Скалярное произведение

Евклидовы и унитарные пространства

Пусть V(K) – ЛП (вещественное или комплексное)

О п р е д е л е н и е. Отображение

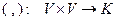
называется скалярным произведением (СП), если оно удовлетворяет следующим аксиомам:

1) ;

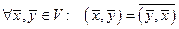2) 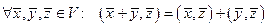; (1.1)

3) .

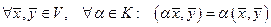4) .

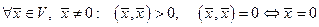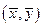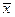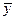Число называется скалярным произведением векторов и , а аксиомы 1)- 4) называются аксиомами скалярного произведения.

Замечание 1. В вещественном случае черта в аксиоме 1) может быть опущена.

Замечание 2. Аксиома 4) на первый взгляд кажется парадоксальной, т.к. знак для комплексных чисел не определен. Однако, из первой аксиомы следует, что скалярный квадрат 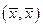есть вещественное число.

Вещественное линейное пространство со скалярным произведением называется евклидовым пространством (ЕП), а комплексное – унитарным пространством (УП).

Обозначение: Е – ЕП, U -УП.

При введении понятия ЕП(УП) мы абстрагируемся не только от природы элементов ЛП, но и от конкретного вида правил образования суммы элементов, правил произведения элемента на число, правил СП элементов (лишь бы эти правила удовлетворяли восьми аксиомам ЛП и четырем аксиомам СП).

Примеры ЕП.

1. 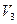- ЛП всех свободных векторов.

.

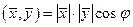2. 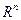- n-мерное ЛПупорядоченных совокупностей n вещественных чисел

, .

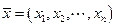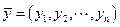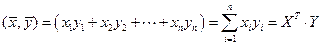. (1.2)

Рассмотренное ЛП обозначается .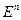

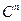- n-мерное ЛПупорядоченных совокупностей n комплексных чисел

. (1.3)

Рассмотренное ЛП обозначается .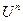

3. В пространстве непрерывных функций 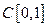скалярное произведение функци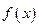й и 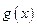может быть задано в виде

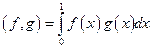(1.4)

Проверить выполнение аксиом самостоятельно.

Скалярные произведения (1.2), (1.3) принято называть обычными скалярными произведениями.

Из определения скалярного произведения вытекают следующие простейшие свойства операции скалярного произведения.

1. .
2. .
3. .
4. 

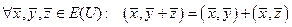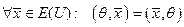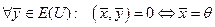
Т е о р е м а 1.1. (Неравенство Коши-Буняковского (К-Б)). Для любых векторов 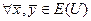имеет место неравенство

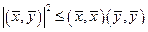. (1.5)

Доказательство. При 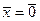неравенство превращается в тождество. Поэтому будем считать, что 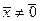. Для любых 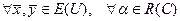в силу аксиом 1)-4) имеем:

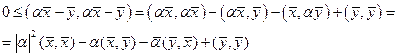(1.6)

Это неравенство должно выполняться для всех 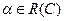, в том числе и для 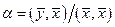(так как 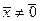, то 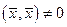). Тогда получим

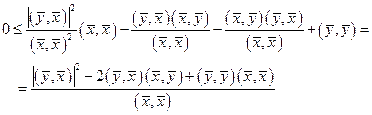
И так как 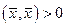, то

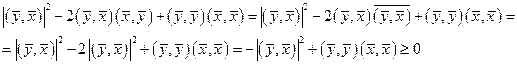
Откуда после получаем неравенство Коши-Буняковского. #

Замечание 3. В евклидовом пространстве неравенство Коши-Буняковского может быть записано в виде

.

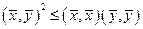Т е о р е м а 1.2. Неравенство К-Б обращается в тождество тогда и только тогда, когда векторы 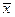и 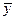коллинеарны.

Доказательство. Действительно, если 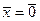, то 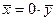. Если 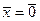, то неравенство (1.6) обращается в равенство тогда и только тогда, когда 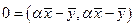, т.е. когда . #

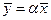2. Метрические характеристики ЕП(УП). Длины и углы.

О п р е д е л е н и е. В ЕП(УП) длиной вектора 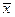называется арифметическое значение квадратного корня из его скалярного квадрата

.

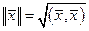Из аксиом скалярного произведения следует:

1) 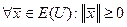, причем 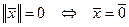, т.е. любой вектор имеет длину.

Следует из аксиомы (4).

2) , : .

.

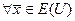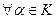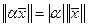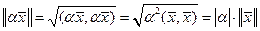В новой терминологии неравенство К-Б может быть записано в виде

. (2.1)

Т е о р е м а 2.1. В ЕП(УП) для любых векторов 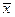и 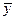имеет место неравенство

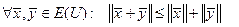. (2.2)

Доказательство.

,

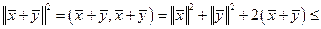
откуда следует (2.2). #

Неравенство (2.2) называется неравенством треугольника в евклидовом(унитарном) пространстве.

О п р е д е л е н и е. В ЕП угол между ненулевыми элементами 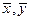— это число 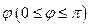, определяемое из уравнения

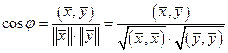. (2.3)

Из неравенства К-Б следует, что угол определен для любых двух ненулевых элементов пространства.

В унитарном пространстве понятие угла между векторами не вводится. Но и в ЕП и в УП можно ввести обобщенние понятия прямого угла.