Дифференциальное уравнение изогнутой оси балки

От действия внешних сил, расположенных в одной из главных плоскостей инерции прямой балки, ось балки изгибается в той же плоскости. При этом точки оси балки получают вертикальные перемещения, а поперечные сечения балки получают некоторые повороты относительно их начального состояния.

Изогнутая ось балки называется упругой линией, а перемещения точек оси балки в направлении нормали к недеформированной оси, называются прогибами балки.

Прогиб оси балки в произвольной точке, расположенной на расстоянии xот начала координат, будем обозначать через v(x).

Угол поворота поперечного сечения балки, который находится на расстоянии x от начала координат, будем обозначать через φ(x).

Прогибы балки принимаются с положительным знаком, если они направлены вверх, а углы поворота имеют положительный знак, если поперечные сечения балки получают повороты, направленные против движения часовой стрелки. Прогибы балки измеряются в единицах длины (м, см), а углы поворота в радианах.

При изгибе балки длина ее оси не изменяется, потому что она расположена в нейтральном слое, где нормальные напряжения равняются нулю. Прогибы и углы поворота являются очень малыми величинами в сравнении с размерами балки.

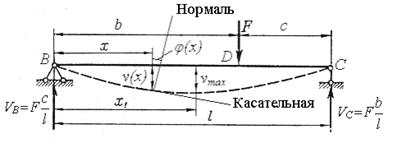
Рис.11.20

На рис.11.20 начерчена прямолинейная ось балки до её нагружения, и криволинейная упругая линия, после нагружения балки. Произвольная точка оси балки, взятая на расстоянии x от начала координат, получает прогиб v(x). Поперечное сечение балки в этой точке получает поворот на угол φ(x). Этот угол равняется углу между касательной к упругой линии в данной точке и осью балки до деформации, или между нормалью к упругой линии в данной точке и поперечным сечением недеформированной балки.

Для определения прогибов и углов поворота необходимо составить дифференциальное уравнение изогнутой оси балки. Для этого используем известную зависимость между радиусом кривизны изогнутой оси балки r и изгибающим моментом M_y, полученной при выводе формулы нормальных напряжений:

,

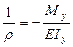а также известную из курса высшей математики зависимость между радиусом кривизны и производными от уравнения изогнутой оси:

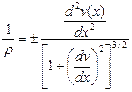
Приравняем правые части двух приведенных зависимостей и учтем, что при действии положительного изгибающего момента вторая производная от уравнения изогнутой оси балки также имеет положительный знак. Тогда будем иметь:

(11.25)

Первая производная от уравнения изогнутой оси балки по абсциссе x, которая содержится в знаменателе левой части зависимости (11.25), есть тангенс угла между осью x и касательной к упругой линии в произвольной точке. Учитывая, что углы поворота очень малые по сравнению с размерами балки (тангенсы этих углов практически не превышают 0,01 радиана), можем пренебречь квадратом первой производной в сравнении с единицей. Тогда дифференциальное уравнение изогнутой оси балки (или упругой линии) будет иметь вид:

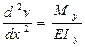(11.26)

или 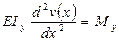(11.27)