Напряжение в поперечных сечениях стержня

Продольная сила N в произвольном поперечном сечении бруса является равнодействующей внутренних усилий в этом сечении. При растяжении или сжатии стержня внутренние усилия действуют в каждой точке сечения. Они направлены перпендикулярно поперечному сечению и имеют название нормальных напряжений σ. Равнодействующая нормальных напряжений действует вдоль оси стержня и равняется продольной силе N.На каждую элементарную площадку dAпоперечногосечения действует элементарная нормальная сила, которая равняется произведению σ∙dA.Учитывая, что таких сил в сечении стержня бесконечное множество и их равнодействующая равняется N, найдем:

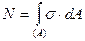(9.1)

В формуле (9.1) σ есть нормальное напряжение в произвольной точке поперечного сечения стержня, а величина Аесть площадь этого сечения.

Определенный интеграл (9.1) по всей площади сечения можно вычислить в случае, если известный закон распределения нормальных напряжений по этой площади, т.е. известна эпюра нормальных напряжений по ширине и высоте сечения. Исследование напряжений при действии осевых сил позволяет сделать вывод, что в сечениях стержня достаточно удаленных от точек нагружения стержня сосредоточенными силами, нормальные напряжения равномерно распределены по всей площади сечения (рис.9.4), то есть напряжение σявляется постоянной величиной. Это обстоятельство позволяет вынести σ за знак интеграла в зависимости (9.1) и в результате получаем:

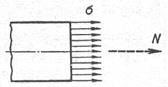
Рис. 9.4

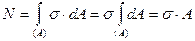, откуда

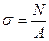(9.2)

Таким образом, нормальное напряжение в произвольной точке поперечного сечения стержня при растяжении (или сжатии) равняется отношению продольной силы N, действующей в этом сечении, к площади A поперечного сечения.

Нормальные напряжения изменяются по длине стержня в зависимости от изменения продольной силы Nи площади сечения A. Если на некотором участке стержня продольная сила и площадь сечения имеют постоянные значения, то напряжение также будет иметь постоянное значение. Эпюра напряжений по длине стержня будет ограничена прямой, параллельной оси стержня. Если продольная сила линейно зависит от положения сечения (при равномерно распределенной нагрузке), а его площадь является постоянной, то напряжение также будет линейно зависеть от положения сечения, то есть эпюра нормальных напряжений будет ограничена прямой, наклоненной к оси стержня под некоторым углом.

Заметим, что эпюра нормальных напряжений имеет скачки в сечениях стержня, где действуют внешние сосредоточенные силы, а также в сечениях, где происходит изменение площади сечения.

Пример 9.2. Определить напряжение в характерных сечениях стержня, рассмотренного в примере 9.1 и построить эпюру этих напряжений по высоте стержня, если площадь верхней части стержня равняется 10 см², а площадь нижней части стержня равняется 20 см².

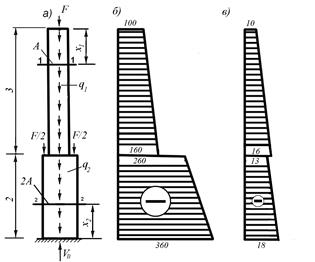
Рис.9.5

Последовательность решения задачи:

1) Используем эпюру продольных усилий, построенную в примере 9.1. Перенесем эту эпюру на рис.9.5,б. и вычислим по формуле (9.2) напряжение в двух сечениях каждого участка стержня: в начале и на конце, поскольку нормальные напряжения, как и продольные силы, линейно зависят от положения сечения.

Для верхней части стержня, длина которого равна 3м, имеем:

при x₁ = 0 - σ = 100 /10 = 10 кН/см² (100 МПа),

при x₁ =3 м - σ = 160 /10 = 16 кН/см² (160 МПа).

Для нижней части стержня имеем:

при x₂ =0 - σ = 360 /20 = 18 кН/см² (180 МПА),

при x₂ =2 м - σ = 260 /20 = 13 кН/см² (130 МПа).

На рис.9.5,в построена эпюра нормальных напряжений.