Расчет СМХ методом угла отсечки.
1.Аппроксимируем ВАХ отрезками прямых.
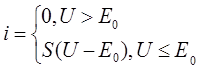 S<0;
S<0;
 i
i
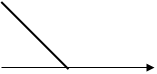 |
E0 u Рис.7.8.
2. Определяем пределы изменения смещения E.
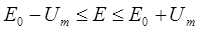
Um – амплитуда несущей.
3. Задаёмся напряжением смещения Е/.
4. Определяем угол отсечки:
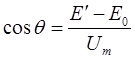
5. Определяем амплитуду первой гармоники:

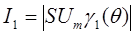 , где g1(q)-коэффициент Берга (см. учебник[1])
, где g1(q)-коэффициент Берга (см. учебник[1])
6.  Возвращаемся в пункт 3 и т.д.
Возвращаемся в пункт 3 и т.д.
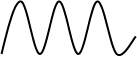
Стандартный вид СМХ показан на рис. 7.9.
Рассмотрим выбор рабочего режима по СМХ.
 I1 I1
I1 I1
 |




 I1max
I1max


 рт I10
рт I10


 I1min
I1min
 | |||
 | |||
Emax Eрт Emin E t
 |
 Рис.7.9.
Рис.7.9.
 uнч
uнч
 |
t
1. Выбираем линейный участок (на глаз).
2. Определяем Еmin , Emax , Imax , Imin .
3. Выбираем рабочую точку в середине линейного участка Р.Т.(I10;ЕР. Т.)
4. Определяем максимальную амплитуду модулирующего сигнала для неискажённой модуляции:
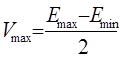
5. Определяем максимальную глубину амплитудной модуля-
ции для неискажённых АМ:
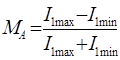
Рассмотрим спектры АМ сигналов при более сложных модулирующих сигналах.
Для простейшего случая , когда модулирующий сигнал представляет собой моногармоническое колебание, спектр модулирующего сигнала показан на рис.7.3 и спектр АМ сигнала на рис.7.4.
Пусть модулирующий сигнал содержит две частоты W1 и W2.
Если спектр модулирующего сигнала более сложный, то усложняется спектр АМ сигнала: он содержит спектр модулирующего сигнала, перенесённый на частоту 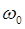 , несущую частоту
, несущую частоту 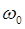 и зеркальное отражение спектра модулирующего сигнала относительно несущей.
и зеркальное отражение спектра модулирующего сигнала относительно несущей.
Спектр модулирующего сигнала.

 U
U
Рис.7.10.
 W1 W2 w
W1 W2 w
Спектр АМ сигнала.
 |
 u Um
u Um
Рис.7.11.
 |  | ||||||
 |  |


 w0-W1 w0 w0+W1 w
w0-W1 w0 w0+W1 w
w0-W2 w0+W2
В этом случае, ширина спектра АМ сигнала 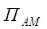 равнаудвоенной максимальной модулирующей частоте :
равнаудвоенной максимальной модулирующей частоте :
Если спектр модулирующего сигнала будет сплошным в некоторой полосе частот:
 |

 U
U

Рис.7.12.
 W1 W2 w
W1 W2 w
то спектр АМ сигнала также будет иметь верхнюю и нижнюю боковые полосы частот , и тоже сплошные:
 u Um
u Um
Рис.7.13.
 |  |


 w0-W1 w0 w0+W1 w
w0-W1 w0 w0+W1 w
w0-W2 w0+W2
Дата добавления: 2016-06-22; просмотров: 2941;











