Уравнение движения для двухфазной жидкости под действием капиллярных сил

Углеводородные системы могут быть гомо- и гетерогенными. В гомогенной системе все ее части имеют одинаковые физические и химические свойства. Составляющие гомогенной системы (называемые компонентами) «размазаны» по всему пространству и взаимодействуют на молекулярном уровне. Для гетерогенной системы физические и химические свойства в разных точках различны. Гетерогенные системы состоят из фаз. Фаза-это часть системы, которая является гомогенной и отделена от других фаз отчетливыми границами. Смесь воды, нефти и газа в пласте-типичный пример гетерогенной среды.

На межфазной границе возникает капиллярный скачок давления рк, определяемый по формуле Лапласа,

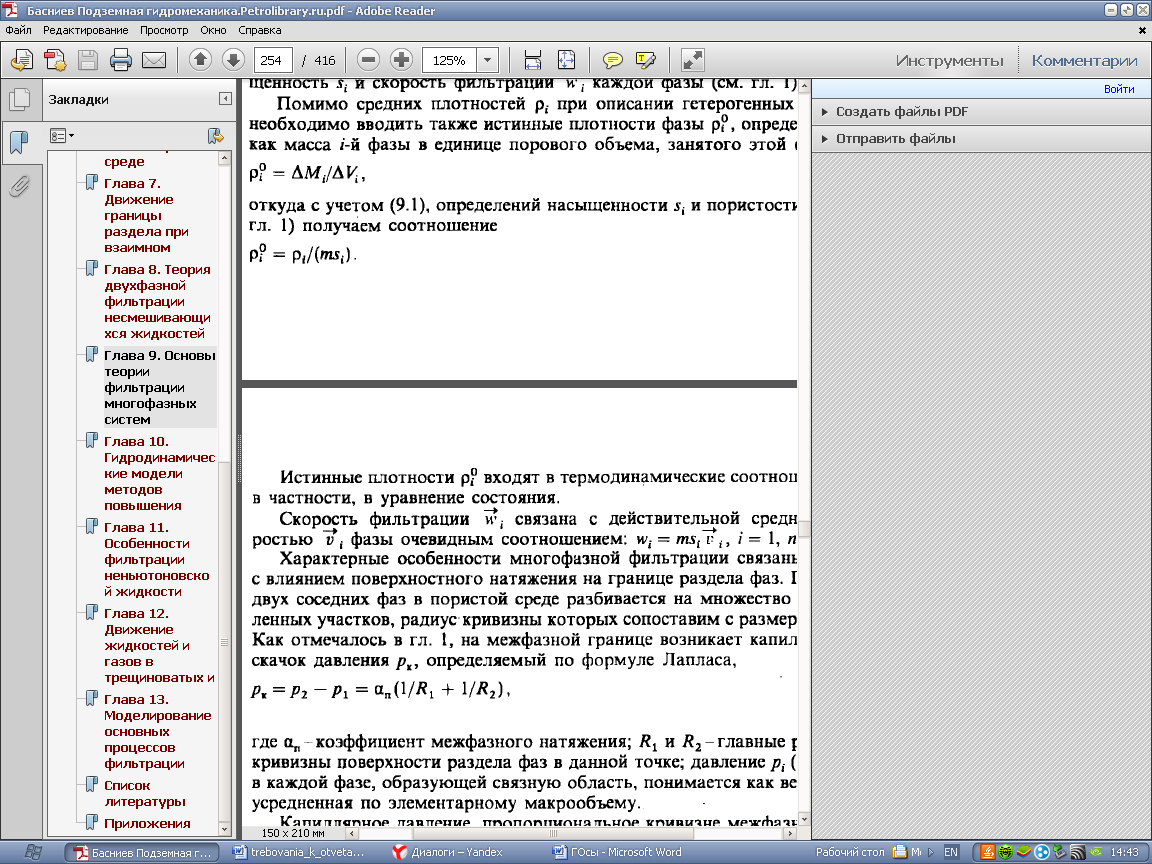
где а - коэффициент межфазного натяжения; R1 и R2- главные радиусы кривизны поверхности раздела фаз в данной точке; давление p (i= I, 2) в каждой фазе, образующей связную область, понимается как величина, усредненная по элементарному макрообъему.

Капиллярное давление, пропорциональное кривизне межфазной границы, зависит от структуры порового пространства и от преимущественной смачиваемости скелета породы каждой из фаз. Капиллярные силы, способные создать в поровых каналах достаточно большие градиенты давления по сравнению с внешним перепадом, полностью определяют распределение фаз в поровых каналах.

При медленной совместной фильтрации можно предположить,что при данной насыщенности жидкости распределены так же, как и в условиях гидростатического равновесия. Это- один из постулатов теории многофазной фильтрации.

Он означает, что при совместном течении жидкостей:

1) разность давлений в двух фазах р2 — Р1 равна капиллярному давлению р_к, которое считается известной экспериментальной функцией

насыщенности, т.е

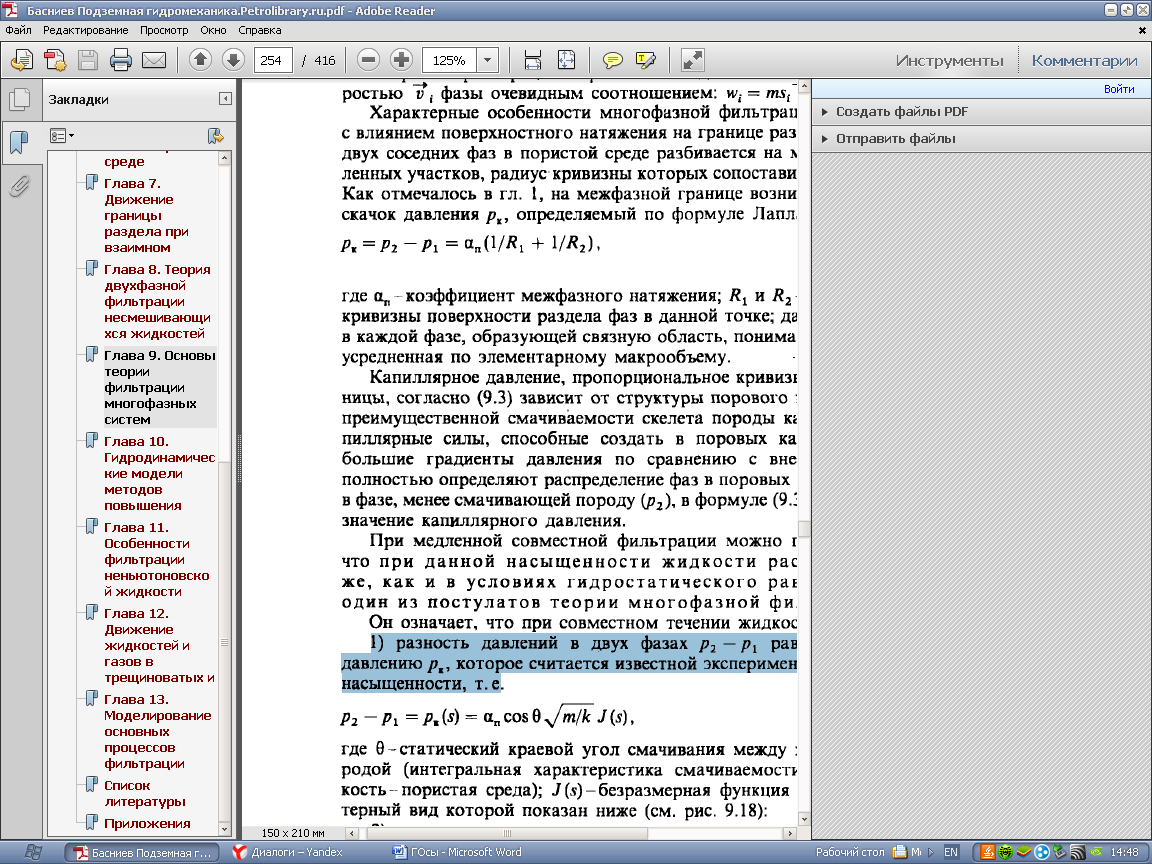
где Ǿ - статический краевой угол смачивания между жидкостями и породой (интегральная характеристика смачиваемости в системе жидкость-пористая среда); J (s) - безразмерная функция Леверетта, харакерный вид

2) капиллярные и гидромеханические силы влияют на распределение

фаз в порах;

3) гидравлические сопротивления, а следовательно, относительные проницаемости каждой из фаз являются однозначно определенными

функциями насыщенности;

4) закон движения каждой из фаз формулируется как обобщенный

закон Дарси

Процессы многофазной фильтрации идут по-разному, в зависимости от характерного времени фильтрационного процесса и от размеров области течения. Капиллярные силы создают в пористой среде перепад давления, величина которого ограничена и не зависит от размеров области фильтрации. Вместе с тем, перепад внешнего давления, создающего фильтрационный поток между двумя точками, пропорционален скорости фильтрации и расстоянию между этими точками. Если размеры области малы, то при достаточно малых скоростях фильтрации капиллярные силы могут превзойти внешний перепад давления.Напротив, если рассчитывается движение в очень большой области(например, в целой нефтяной или газовой залежи), то влияние капиллярных сил на распределение давления незначительно и их действия сказываются через локальные процессы перераспределения фаз. Взаимное торможение фаз, благодаря которому относительные фазовые про-

ницаемости не равны соответствующим насыщенностям, обусловлено, тпрежде всего, капиллярными эффектами. В тех случаях, когда можно пренебречь капиллярным скачком px{s), капиллярность косвенно учитывается самим видом опытных кривых относительных фазовых проницаемостей kt(s).

Уравнение движения фазРассмотрим фильтрацию флюидов в пористых средах, принимаяв качестве закона движения линейный закон фильтрации Дарси .Закон Дарси записан в конечном виде, т.е. для пласта или образца с постоянной площадью сечения, где Ар* -разность приведенных давлений на конечной длине L. Для трубки тока с переменной площадью сечения по длине трубки закон Дарси записывается в дифференциальной форме.

Выделим два сечения - первое на расстоянии х от начала отсчета вдоль линии тока, второе-на расстоянии Ах от первого .Пусть движение флюида происходит в направлении возрастания координаты х.

В сечении с координатой х обозначим приведенное давление через

р* (S, t), в сечении с координатой х + ∆S-через р* (s + ∆S , t). Использовав

формулу получим:

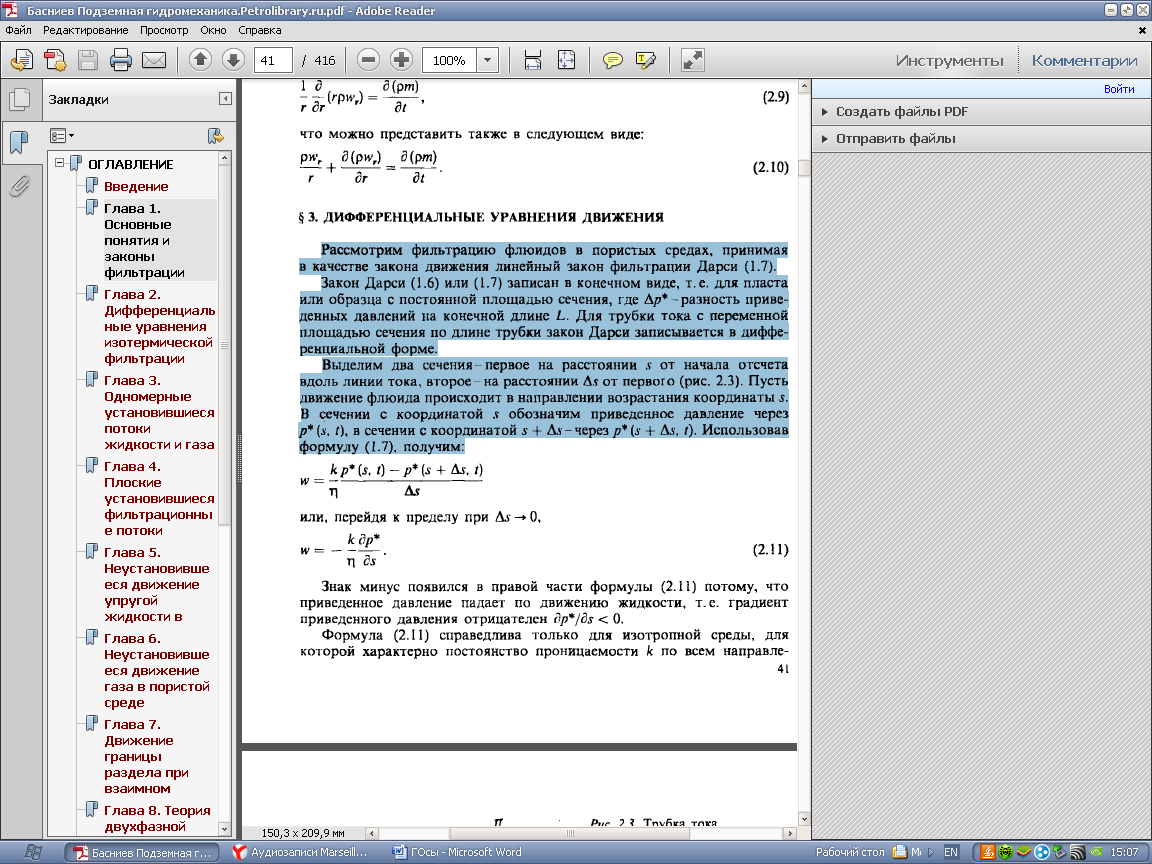
Знак минус появился в правой части формулы потому, что приведенное давление падает по движению жидкости, т.е. градиент приведенного давления отрицателен Dp*/Dх < 0.