Прогнозирование (проектирование) технологических показателей разработки (нефтеизвлечения) на основе аналитической модели процесса

Под прогнозированием понимается установление заключения о предстоящем развитии, т. е. предсказание о течении технологического процесса разработки в будущем. Следовательно, к методам прогнозирования относят все методы моделирования процесса разработки.

Различают физическое и математическое моделирования.

При физическом моделировании на модели, представляющей по существу натурный или масштабно уменьшенный образец оригинала (лабораторную, пилотную установки), воспроизводят и исследуют процессы, качественно одинаковые с процессами, протекающими в реальном объекте.

Математическое моделирование заключается в исследовании процессов путем построения и решения системы математических уравнений, относящихся к собственно процессу и краевым условиям.

Системы математических уравнений решают аналоговым и вычислительным методами. Аналоговый метод математического моделирования базируется на подобии явлений и процессов различной физической природы, т. е. на широкой физической аналогии. Вычислительные методы подразделяются на аналитические, численные и статистические.

Аналитические методы соответствуют классическому подходу к моделированию процессов, когда ставится исходная задача, вводятся упрощающие предположения и на их основе формулируется новая задача, которая поддается решению в виде аналитического выражения, формулы, обеспечивающей получение значения функции для каждого значения аргумента. Упрощающие предположения иногда приводят к существенным погрешностям в результатах проектирования, а без них задача в аналитической форме не решается. К числу аналитических методов, дающих точные решения задач разработки нефтяных месторождений, т. е. в точности удовлетворяющих исходным уравнениям, начальным и граничным условиям, относятся метод разделения переменных (метод Фурье), методы теории функций комплексного переменного, интегральных преобразований и др. Приближенные решения получают с использованием методов эквивалентных фильтрационных сопротивлений, последовательной смены стационарных состояний, интегральных соотношений и др.

Метод эквивалентных фильтрационных сопротивлений – основной аналитический метод определения количественной связи между дебитами скважин и давлениями на их забоях и на контуре питания пласта (нагнетания воды) в условиях жесткого водонапорного режима. Сущность метода состоит в замене полного фильтрационного сопротивления реального потока жидкостей сложной конфигурации несколькими эквивалентными (равнозначными) последовательными или параллельными фильтрационными сопротивлениями простейших (прямолинейно-параллельных, плоскорадиальных) потоков. Такая замена вносит определенную погрешность в результаты расчета, которая, однако, допустима при недостаточной точности исходной геологопромысловой информации.

Дебиты соответственно прямолинейного и кругового рядов:

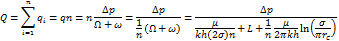
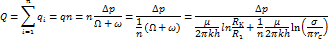
Отсюда следует, что приток ко всем скважинам можно рассматривать как параллельное соединение проводников с одинаковыми сопротивлениями (Ω+ω). Таким образом, фильтрационный поток к скважинам можно представлять эквивалентной схемой электрических сопротивлений и для расчета использовать законы Ома и Кирхгофа (первый или второй закон), подразумевая в соответствии с принципом ЭГДА под силой тока, разностью напряжений и электрическими сопротивлениями их аналоги – расход жидкости, перепад давлений, фильтрационные сопротивления.

Метод эквивалентных фильтрационных сопротивлений можно применять при граничных положениях ВНК, т. е. когда в пласте движется только нефть или только вода (после полного обводнения). На использовании метода эквивалентных фильтрационных сопротивлений основаны методики ВНИИ-1, ТатНИПИнефть и др.

Процесс разработки конкретного нефтяного месторождения однократен и непосредственному наблюдению «доступен» только в ограниченном числе скважино-точек. Это обусловило развитие методов его моделирования, как непрямых, опосредствованных методов научного исследования. Моделирование, и как результат, модель процесса обеспечивают возможность при сравнительно небольших затратах в короткие сроки многократно (многовариантно) «проиграть» медленно протекающие процессы разработки в различных технологических условиях и тем самым выбрать рациональную технологию. При создании моделей процесса разработки нефтяных месторождений моделируют геолого-физические свойства пласта, его геометрическую форму, флюиды и процесс извлечения нефти и газа из недр.

Различают физическое и математическое моделирования. При физическом моделировании на модели, представляющей по существу натурный или масштабно уменьшенный образец оригинала (лабораторную, пилотную установки), воспроизводят и исследуют процессы, качественно одинаковые с процессами, протекающими в реальном объекте.

Математическое моделирование заключается в исследовании процессов путем построения и решения системы математических уравнений, относящихся к собственно процессу и краевым условиям. Математическая модель основана на упрощении (идеализации) сложного реального процесса. Для ее создания природные условия соответствующим образом дифференцируют, выделяют среди них главные, определяющие факторы и представляют их в таком виде, который обеспечивает возможность достижения цели. Причем нефтегазоносный пласт рассматривают как единую гидродинамически связанную систему не только во всей области нефтегазоносности, но и включая окружающую водонапорную область. Перемещение флюидов внутри этой единой системы определяется начальными (до начала разработки) и граничными (на поверхностях, ограничивающих пласт с внешних сторон, и на стенках скважин внутри пласта) условиями или в совокупности краевыми условиями.

Системы математических уравнений решают аналоговым и
вычислительным методами. Аналоговый метод математического
моделирования базируется на подобии явлений и процессов различной физической природы, т. е. на широкой физической аналогии. Можно назвать аналогии между полями фильтрации жидкости (закон Дарси), электрического тока в проводящей среде (закон Ома), электрическим в диэлектрике (закон индукции), магнитным (закон магнитной индукции) и температурным (основное уравнение теплопроводности).

Электрическое моделирование процесса разработки основано
на электрогидродинамической аналогии (ЭГДА), т. е. аналогии между движением электрического тока в проводящей среде и фильтрацией жидкости в пористой среде.

Вычислительные методы подразделяются на аналитические, численные и статистические. Аналитические методы соответствуют классическому подходу к моделированию процессов, когда ставится исходная задача, вводятся упрощающие предположения и на их основе формулируется новая задача, которая поддается решению в виде аналитического выражения, формулы, обеспечивающей получение значения функции для каждого значения аргумента. Упрощающие предположения иногда приводят к существенным погрешностям в результатах проектирования, а без них задача в аналитической форме не решается. К числу аналитических методов, дающих точные решения задач разработки нефтяных месторождений, т. е. в точности удовлетворяющих исходным уравнениям, начальным и граничным условиям, относятся метод разделения переменных (метод Фурье), методы теории функций комплексного переменного, интегральных преобразований и др. Приближенные решения получают с использованием методов эквивалентных фильтрационных сопротивлений, последовательной смены стационарных со-
стояний, интегральных соотношений и др.

Статистические методы моделирования базируются на статистических данных предшествующей разработки месторождений. Изучая фактические закономерности развития процесса в залежи за прошедший период (ретроспективу), они позволяют оперативно без больших затрат времени и труда сформулировать заключение о предстоящем развитии основных технологических показателей разработки (перспективу).

Численные методы заключаются в определении с помощью ЭВМ
численных значений функции в некоторых дискретных точках
для заданных численных значений аргумента, т. е. решение получается в некоторых точках пространства. Для этого пространственная область фильтрации мысленно разделяется на ряд квадратов или блоков путем наложения сетки определенного типа (в большинстве равномерной квадратной сетки). Исследуемый интервал времени также разделяется на отдельные элементарные интервалы с постоянным шагом. Преобразование непрерывных дифференциальных уравнений к дискретному виду осуществляется с помощью метода конечных разностей. Получить конечно-разностные уравнения можно методом разложения функции в ряд Тейлора в заданной точке, решая уравнение относительно искомой производной.

Математическую модель процесса разработки нефтяного месторождения составляют совместно модель пласта и модель процесса извлечения нефти.

Модель пласта — это система количественных представлений
о его геолого-физических свойствах, используемая в расчетах
разработки нефтяного месторождения

С развитием теории разработки нефтяных месторождений
представления о моделях пластов изменялись, усложнялись модели пластов, учитывалось большее число факторов реального пласта. Одна из первых моделей пласта — модель однородного по параметрам пласта. Она реализует гипотезу об однородности пласта как по площади, так и по вертикальному разрезу залежи. Главные параметры модели — это абсолютная проницаемость, пористость, нефтенасыщенность и эффективная толщина. Их определяют по данным промыслово-геофизических исследований скважин. С использованием кернов определяют пористость, абсолютную проницаемость и реже нефтенасыщенность.
Затем устанавливают статистическую связь между результатами лабораторных и промыслово-геофизических исследований (обычно в виде количественных зависимостей). По этим зависимостям определяют средние значения изучаемых параметров в каждой скважине, которые усредняют для пласта в целом.
При таком построении модель является вероятностно-статистической. Для построения ее можно использовать также результаты гидродинамических исследований скважин и пластов. Такая модель позволяла получить относительно строгие аналитические выражения для расчета процессов движения флюидов.
Однако, сочетая модель однородного пласта с моделью поршневого вытеснення нефти, устанавливали, что разработка месторождения при заводнении может осуществляться без отбора воды. Такое в принципе противоречит фактическим данным. Это привело к тому, что нашли распространение модели слоисто-неоднородного пласта.

Модель слоисто-неоднородного пласта включает в себя серию (два или более) пропластков (слоев) разной проницаемости, которые либо разделены практически непроницаемыми тонкими пропластками, либо гидродинамически свободно сообщаются между собой, либо частично сообщаются между собой.
Обычно используется первая модификация. Пласт может характеризоваться закономерным или обычно вероятностным (случайным) распределением проницаемости слоев в разрезе. Построение модели аналогично предыдущему, однако при этом необходимо определение параметров не только пласта в целом по скважинам, но и отдельных его слоев. Для этого используются методы детальной корреляции разрезов пластов, промыслово-геофизических и лабораторных исследований, а также изучения профилей притока (отбора) в добывающих скважинах и приемистости (поглощения, закачки вытесняющего агента) в нагнетательных скважинах (глубинная дебито-, расходо- или термометрия).

Модель зонально-неоднородного пласта представляет реальный неоднородный пласт состоящим из зон различной проницаемости. Дальнейшим развитием этой модели было принятие большого числа хаотически расположенных зон, обладающих различными свойствами.

Различное сочетание рассмотренных моделей пластов и моделей процесса извлечения нефти определило создание конкретных моделей процесса разработки и методик расчета. Методикой расчета называют процедуру выполнения вычислений на основе принятой модели. Ввиду большой сложности механизма многофазной фильтрации в неоднородных пластах и соответственно исходной системы описывающих ее дифференциальных уравнений, сначала развивались аналитические методы расчета, которые в основном сводились к приближенному решению уравнений при тех или иных допущениях и краевых условиях. Различные предпосылки и подходы многих авторов к решению одной и той же задачи привели к созданию значительного количества разных методик расчета технологических показателей.

Методика должна быть достаточно универсальной в смысле учета многообразия режимов разработки (водо-, газонапорный, режим растворенного газа или их возможные сочетания) и учета неодномерности фильтрационных потоков.

Методика должна учитывать неоднородность пласта по проницаемости, коэффициент продуктивности (приемистости) скважин, характер работы скважин (неодновременный ввод скважин в эксплуатацию, перевод добывающих скважин в нагнетательные, отключение обводнившихся и загазовавшихся скважин, изменение забойных давлений и дебитов нефти, жидкости, газа, коэффициента эксплуатации скважин во времени), а также особенности работы скважинного оборудования, обеспечивающего подъем продукции на поверхность.