Систематические и случайные ошибки.
Измеряя любую физическую величину с помощью прибора с конкретной ценой деления w, нам приходилось округлять результат до ближайшего целого деления или хотя бы до значения, соответствующего середине между соседними делениями. Погрешность, которую мы считали равной 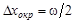 , можно назвать по сути ошибкой округления. Эта ошибка присутствует всегда и включается в общий класс систематических ошибок. Можно ли ее уменьшить? Конечно, можно взять более дорогой и точный прибор.
, можно назвать по сути ошибкой округления. Эта ошибка присутствует всегда и включается в общий класс систематических ошибок. Можно ли ее уменьшить? Конечно, можно взять более дорогой и точный прибор.
Кроме ошибки округления существует предельная ошибка прибора, связанная с неточностью изготовления шкалы на заводе. Неужели кто-то поверил, что интервал на шкале линейки действительно соответствует 1 мм? Конечно нет. Цена деления миллиметровой линейки приблизительно равна 1мм. И эта приблизительность выражается в предельной ошибке, прописанной в заводском паспорте прибора. Допускаемая предельная погрешность, например, для стальной линейки длиной 300 мм составляет 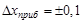 мм. И чем длиннее линейка, тем больше приборная погрешность. Для упрощения обработки данных, мы будем учитывать только ошибку округления и пренебрежем приборной.
мм. И чем длиннее линейка, тем больше приборная погрешность. Для упрощения обработки данных, мы будем учитывать только ошибку округления и пренебрежем приборной.
При измерении интервалов времени с помощью секундомеров вводится систематическая ошибка, которая связана с реакцией человека на нажатие кнопки. Один человек медлителен от природы и нажимает кнопку на секундомере позже начала процесса, второй наоборот – слишком рано. Медицинские исследования этого вопроса дают среднее значение абсолютной погрешности измеряемого интервала 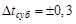 с при нажатии кнопки в начале и в конце процесса. Такую ошибку называют субъективной. Вот оно что! Тогда понятен большой разрыв между двумя одновременными измерениями падения кирпича (см. 2.2.1). Его можно объяснить разной реакцией у меня и у моего напарника.
с при нажатии кнопки в начале и в конце процесса. Такую ошибку называют субъективной. Вот оно что! Тогда понятен большой разрыв между двумя одновременными измерениями падения кирпича (см. 2.2.1). Его можно объяснить разной реакцией у меня и у моего напарника.
А какие еще ошибки бывают, кроме систематических?
Для ответа на этот вопрос проведем (мысленно) лабораторную работу по измерению дальности полета маленького шарика, выпущенного пружинным пистолетом под углом a к горизонту. Будем стрелять 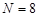 раз, при этом шарик будет оставлять следы на бумаге (для этого нужно всего лишь положить копировальную бумагу поверх простого листа).
раз, при этом шарик будет оставлять следы на бумаге (для этого нужно всего лишь положить копировальную бумагу поверх простого листа).
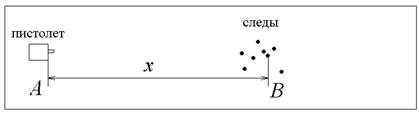
Рис.19. Схема эксперимента по измерению дальности полета шарика.
Проведем черту А перпендикулярно оси пистолета (рис.19), соответствующую начальной координате шарика. Параллельно линии А проведем линию В через одну из точек-следов. Измерим расстояние хi между ними и будем называть эту величину дальностью полета. Запишем пример таких измерений:
Таблица 3. Измерения дальности полета шарика с помощью линейки.
| хi, мм |
Почему же результаты отличаются, ведь используется каждый раз один и тот же пистолет и один и тот же шарик? Чтобы не было ветра, я закрыл окно, а разброс данных остался. Может дело в пружине? Заряжая пистолет, каждый раз пружина сжимается немного по-разному? Может шарик каждый раз немного меняет свою траекторию в стволе? А вот это я уже не смогу никак учесть! Сжатие пружины и траектория шарика совершенно случайные величины в этой установке. Таким образом, разброс данных можно объяснить случайностью, и поэтому вводится класс случайных величин, а с ними вместе и особый вид случайных ошибок.
Для обработки набора данных случайной величины вводится среднее значение
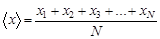
и среднеквадратичное отклонение от среднего
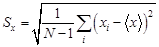 ,
,
Используя данные из табл.3, получим
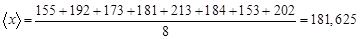 мм
мм
Если кто-то думает, что списав все цифры с калькулятора, можно получить более точный ответ, я напомню о цене деления линейки и о систематической погрешности округления. Никакого смысла нет тащить за собой цифры в разрядах дальше десятых, потому что ошибка округления 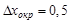 мм. И вообще можно ввести жесткое требование к количеству знаков в числах при рассчетах. В промежуточных рассчетах надо оставлять на одну цифру больше, чем количество цифр в исходных данных. Последняя цифра будет запасной и поможет в конце измерений сделать грамотное округление конечного результата. Таким образом, достаточно ограничиться значением
мм. И вообще можно ввести жесткое требование к количеству знаков в числах при рассчетах. В промежуточных рассчетах надо оставлять на одну цифру больше, чем количество цифр в исходных данных. Последняя цифра будет запасной и поможет в конце измерений сделать грамотное округление конечного результата. Таким образом, достаточно ограничиться значением
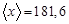 мм.
мм.
Добавим к табл.3 еще одну строку, где запишем отклонение каждого значения 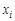 от среднего
от среднего 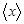 , т.е.
, т.е. 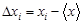
Таблица 4. Измерения дальности полета шарика с помощью линейки.
| хi, мм | ||||||||
| Δxi=xi – <x>, мм | – 26,6 | 10,4 | – 8,6 | – 0,6 | 31,4 | 2,4 | – 28,6 | 20,4 |
Отклонения от среднего могут быть как положительные, так и отрицательные. Это и понятно: среднее значение 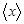 всегда лежит где-то посередине набора значений
всегда лежит где-то посередине набора значений 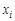 , поэтому оно больше одних значений и меньше других. Для рассчета среднеквадратичного отклонения
, поэтому оно больше одних значений и меньше других. Для рассчета среднеквадратичного отклонения 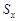 надо сложить квадраты отклонений
надо сложить квадраты отклонений 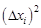 и разделить на
и разделить на 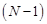 , не забыв потом взять квадратный корень из результата:
, не забыв потом взять квадратный корень из результата:
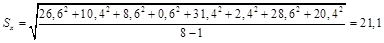 мм
мм
Оказывается, если проделать несколько таких серий по 8 выстрелов, то в каждой серии будет свое среднее значение дальности полета 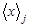 , а среднеквадратичное отклонение этих средних значений
, а среднеквадратичное отклонение этих средних значений 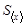 будет намного меньше, чем
будет намного меньше, чем 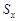 (для простоты будем считать, что среднеквадратичные отклонения в каждой серии равны друг другу) и равно
(для простоты будем считать, что среднеквадратичные отклонения в каждой серии равны друг другу) и равно
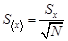
В нашем примере оно равно 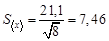 мм. Эту величину грубо можно принять за доверительный интервал
мм. Эту величину грубо можно принять за доверительный интервал 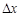 , в который должно попасть точное значение дальности полета шарика, т.е.
, в который должно попасть точное значение дальности полета шарика, т.е. 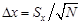 . Относительная погрешность вычисляется по формуле
. Относительная погрешность вычисляется по формуле
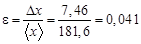 или 4,1%
или 4,1%
В лабораторном журнале надо записать ответ
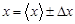
или для нашего примера 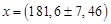 мм.
мм.
Теперь надо вспомнить об округлении результата, Так как погрешность наблюдается в разряде целых, то запись ответа станет такой:
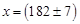 мм
мм 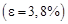
Можно ли уменьшить случайную погрешность? Формула 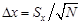 говорит нам, что увеличивая число измерений в эксперименте, можно уменьшить случайную погрешность чуть ли не до 0 (если
говорит нам, что увеличивая число измерений в эксперименте, можно уменьшить случайную погрешность чуть ли не до 0 (если 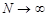 ). И что, тогда мы узнаем точное значение? Как бы не так! Не забывайте о систематической ошибке округления, которая при уменьшении случайной ошибки сама не уменьшается и выходит на первый план.
). И что, тогда мы узнаем точное значение? Как бы не так! Не забывайте о систематической ошибке округления, которая при уменьшении случайной ошибки сама не уменьшается и выходит на первый план.
Таким образом, возникает некоторая сложность в написании ответа, так как в эксперименте есть два типа ошибок – случайные и систематические. Ответ прост: выбирайте ту, которая намного больше. А если они одного порядка, т.е. сравнимы друг с другом? Тогда, складывая квадраты этих огрешностей, объединим их в одну погрешность:
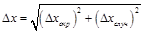
Дата добавления: 2016-06-22; просмотров: 2327;











