Физические условия возникновения невесомости. Продолжение

Состояние невесомости может быть следствием ряда обстоятельств.

Жюль Верн в своем романе «Из пушки на Луну» нарисовал увлекательную картину межпланетного путешествия, допустив при этом, что вполне закономерно и простительно, ряд просчетов. В частности, он считал, что состояние невесомости наступит лишь в то время, когда сила притяжения Земли будет равна силе притяжения Луны и, таким образом, тело будет лишено действия сил притяжения. Вместе с тем, для того чтобы ощутить момент, когда силы притяжения уравновесятся, следовало бы создать гипотетическую лестницу между Землей и Луной (рис. 63).

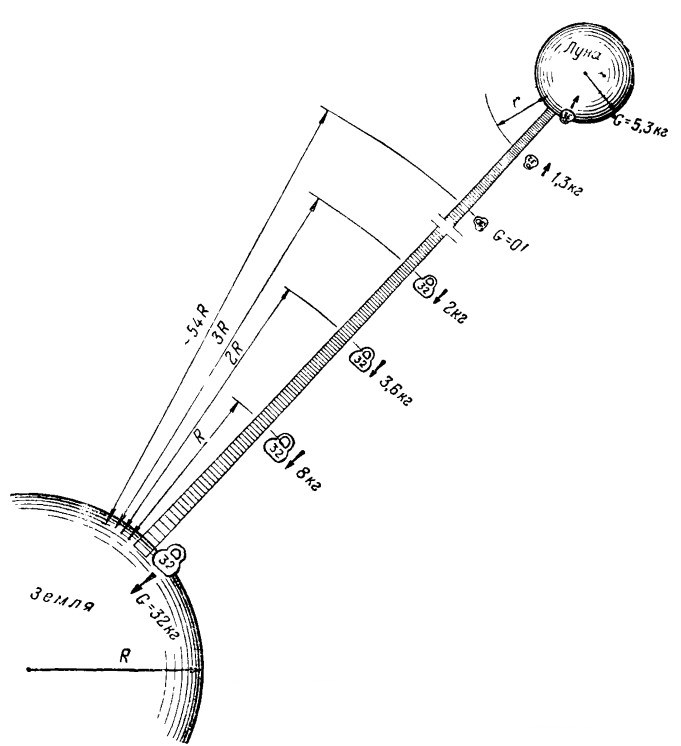
Рис. 63. Изменение величины силы тяжести по мере удаления от Земли и приближения к Луне

Сила тяжести по мере удаления от Земли постепенно бы уменьшалась. Наконец, на расстоянии 346 400 км от Земли силы тяготения уравновесятся, а при дальнейшем подъеме сила тяжести была бы направлена к Луне (рис. 64).

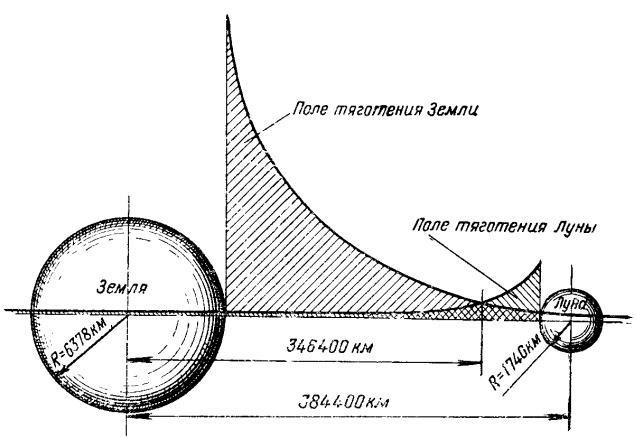
Рис. 64. Взаимодействие полей тяготения Земли й Луны

Действительно, на расстоянии 346 400 км от Земли создаются условия невесомости, но эта точка — чисто математическое понятие. В космическом Полете к Луне эта точка замечена не будет, так как с момента выключения двигателя ракеты в течение всего полета при условии отсутствия сопротивления среды никаких внешних сил (кроме силы тяжести) на ракету действовать не будет — она и все в ней находящееся станет невесомым.

Итак, всякое падение до тех пор, пока сопротивление среды в связи с ростом скорости не окажет своего влияния, характеризуется невесомостью. Так как в наземных условиях нас во всех случаях окружает достаточно плотная материальная среда и любое движение сопровождается преодолением некоторого сопротивления этой среды, невесомость, если и проявляется, то не абсолютная и в течение очень короткого времени.

Возьмем, к примеру, прыжок парашютиста. Выпрыгнув из самолета, он попадает под поток воздуха, который давит на тело с силой, иногда гораздо большей веса человека. О какой невесомости может в этом случае идти речь? Даже при прыжке с аэростата состояние невесомости продлится только несколько секунд. Ведь под действием силы тяжести скорость падения парашютиста будет нарастать, появится сопротивление воздуха, заметное уже на 3—4-й секунде.

Достаточно сказать, что через 11 —12 сек падения сопротивление воздуха полностью уравновесит силу тяжести и тело перестанет падать ускоренно: скорость тела будет иметь постоянную величину, равную скорости в момент наступления равновесия. В этом случае воздух будет такой же опорой парашютисту, какой является он для самолета и какой служит вода для плота, лодки или корабля.

Однако для того чтобы воздух стал достаточной опорой парашютисту, скорость его движения должна быть соответствующей величины, например 42—48 м/сек у земли.

Скоростные самолеты, летящие параллельно земной поверхности, теряют часть своего веса благодаря центробежной силе.

Выше мы говорили, что центробежная сила является реальной для его связей, а не для самого тела. Как же нереальная сила может изменить вполне реальную силу тяготения? Оказывается, может. Все зависит от системы отсчета, по отношению к которой мы рассматриваем силы. Например, центробежная сила вращающегося маховика какой-либо машины не является внешней силой, приложенной к этой машине. Но если мы систему отсчета расположим на оси маховика, то по отношению к ней центробежные силы являются вполне реальными. Под действием этих сил может произойти разрушение маховика и других вращающихся частей механизмов. С полетом самолета или искусственного спутника Земли дело обстоит несколько сложнее, но суть его та же.

Рассмотрим полет самолета параллельно земной поверхности, т. е. по окружности очень большого радиуса. По отношению к Земле на самолет, кроме подъемной силы, сопротивления, тяги двигателей и сил притяжения, никаких внешних сил не действует, и движение самолета определяют только перечисленные силы. В данном случае центробежная сила является фиктивной и не определяет движение самолета. Вот если систему отсчета мы расположим в центре тяжести самолета и заставим ее двигаться вместе с самолетом по круговой траектории, тогда центробежная сила может считаться реальной, направленной против силы притяжения и уменьшающей силу тяжести.

К примеру рассмотрим полет искусственного спутника Земли по круговой орбите. На него действует только сила притяжения Земли, под действием которой спутник искривляет траекторию своего полета и стремится упасть на Землю. Но скорость спутника вдоль поверхности Земли такова, что, падая, он не успевает приблизиться к поверхности Земли и поэтому его траектория представляет окружность, или в общем случае — эллипс.

Если же рассматривать спутник и силы, действующие на него по отношению к системе отсчета, связанной с ним и двигающейся по круговой орбите, тогда, кроме силы притяжения, на него будет действовать и центробежная сила, уравновешивающая силу притяжения. Итак, по отношению к системе отсчета, связанной со спутником, силы, действующие на него (включая в этом случае и центробежную силу), будут уравновешены.

Определим, как изменится вес самолета и его частей в зависимости от скорости полета. Для этого вычислим отношение веса самолета в полете к весу его на земле:

Самолет потеряет, таким образом, около 0,1% своего веса, что не имеет практического значения. При скорости самолета 1000 м/сек имеет место существенное уменьшение веса, сказывающееся на увеличении дальности полета. Если скорость летательного аппарата будет равна 4000 м/сек, то его вес уменьшится на ¼ , а при скорости около 5500 м/сек — вдвое!

По мере дальнейшего увеличения скорости вес тела будет уменьшаться, а при скорости около 7910 м/сек (29 000 км/час) станет равным нулю:

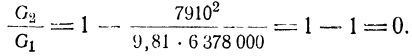
Как известно, такая скорость движения тела называется круговой, так как траектория тела в этом случае представляет собой окружность. Тело, движущееся с круговой скоростью, уже не упадет на Землю. Оно превратится в искусственный спутник Земли (рис. 65). Круговые скорости по мере увеличения высоты над Землей уменьшаются, так как уменьшается сила притяжения.

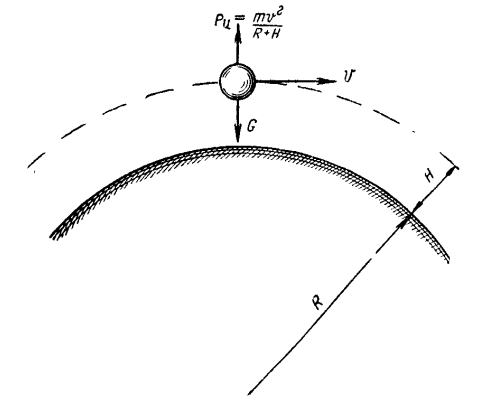
Рис. 65. Уравновешивание силы тяжести центробежной силой: Р_ц — центробежная сила; v — круговая скорость; G — сила тяжести

Круговая скорость на уровне поверхности Земли называется первой космической скоростью. Значения круговой скорости для разных высот приведены в табл. 6.

Интересно отметить, что при высоте круговой орбиты над поверхностью Земли 35870 км период обращения спутника вокруг Земли составит ровно 24 часа, т. е. равен периоду обращения Земли вокруг своей оси. Спутник, запущенный в восточном направлении и вышедший на круговую орбиту, лежащую в плоскости экватора на высоте 35870 км, находился бы, таким образом, все время над одной и той же точкой земной поверхности.

Если скорость тела будет превышать круговую скорость для данной высоты, то тело будет совершать полет не по круговой, а по эллиптической орбите (рис. 3). Один из фокусов этого эллипса совмещен с центром Земли. Точка траектории, максимально приближенная к поверхности Земли, называется перигеем, а максимально удаленная — апогеем. Скорость движения по эллиптической траектории непрерывно меняется: в перигее она максимальная, а в апогее — минимальная.

На высоте полета искусственных спутников сопротивление их движению почти полностью отсутствует. Поэтому их полет происходит без затраты энергии очень длительное время. Так, уже первый советский искусственный спутник просуществовав 93 суток и выполнив 1400 оборотов вокруг Земли, пролетел около 60 миллионов километров! Все это время спутник практически находился в состоянии невесомости. Практически потому, что некоторое сопротивление своему движению он все-таки испытывал. Это сопротивление составляло только тысячные доли грамма, что и позволило спутнику без затраты энергии (помимо необходимой для вывода на орбиту) пролететь такое большое расстояние. Таким образом, невесомость в этом случае не была абсолютной, но практически могла считаться такой.

При движении по орбитам, находящимся выше 2500—3000 км над земной поверхностью, где нет и следов земной атмосферы, движение запущенного спутника будет вечным, а состояние невесомости — абсолютным.

Но вернемся к определению веса тела. Как известно, сила веса выражается формулой

Эта формула справедлива для случая, когда тело находится только в поле действия силы тяжести и никакие ускорения на него не действуют. В формулу, выражающую величину силы веса, следовало бы в общем виде вместо члена g ввести сумму ускорений, действующих на тело по вертикальной оси. Но так как любое ускорение всегда есть следствие действия силы, удобнее вес тела выразить через действующие на него силы.

Такой силой в обычных земных условиях является реакция опоры тела против падения — будь то пол, стул, земля, вода или воздух.

В общем случае, если на тело массой М действует суммарная сила ∑Р, вес элемента тела с массой т будет равен

Для наземных условий это кажется парадоксальным, но направление силы веса обратно направлению реакции, независимо от «низа» и «верха». Так как в обыденной жизни мы редко сталкиваемся с силами, соизмеримыми с силой тяжести, то плохо представляем, что вес может быть направлен, например, не вниз, а вперед. Такой случай нам представляется в мчащемся автобусе, если он резко затормозит.

Суммарная внешняя сила будет результирующей реакции силы тяжести и силы, вызвавшей торможение и распределенной между всеми телами, участвующими в движении, в соответствии с их массой. По закону механики сила действия равна по величине силе противодействия (инерции), направленной в противоположную сторону. Вместо реальных сил можно рассматривать фиктивные силы, силы инерции. Как видно из рис. 66, результирующая силы тяжести и силы инерции проходит далеко за ступнями стоящего человека, что может вызвать его падение, если он не выставит ногу вперед и не удержится руками.

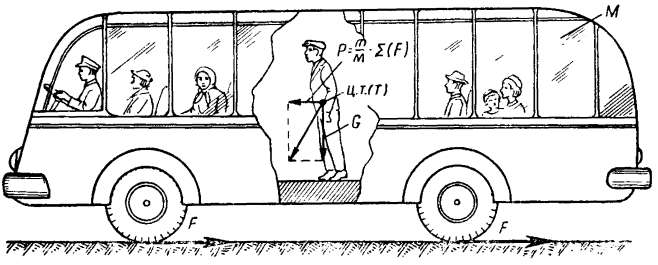
Рис. 66. Изменение величины и направления силы веса тела при приложении к нему внешней силы

В условиях космоса при отсутствии внешних сил вес, как известно, исчезнет, а в случае наличия тяги двигателя или сопротивления среды вес появится; при этом его величина и направление могут быть самыми разнообразными.

Рассмотрим для примера ощущения пассажира на космическом корабле при полете вокруг Земли. Для простоты представим себе двухступенчатую ракету.

В момент взлета по вертикали вверх (рис. 67, а) ракета полностью заполнена топливом и поэтому движется со сравнительно малым ускорением. Но мере выгорания топлива ускорение будет увеличиваться, космонавты будут ощущать все больший и больший вес своего тела (рис. 67, б). Поскольку ракета движется вертикально вверх и силы инерции по направлению совпадают с направлением силы тяжести, ощущения «верха» и «низа» будут соответствовать их действительному положению.

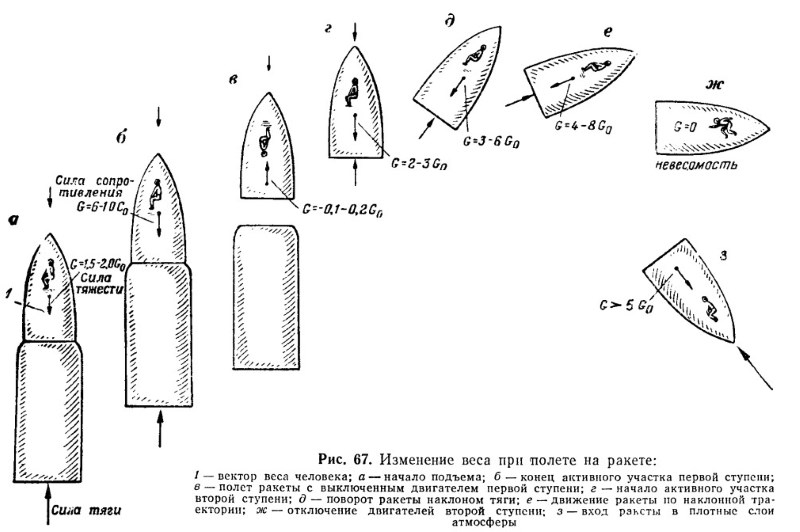
Когда сгорит все топливо первой ступени и двигатель перестанет создавать тягу, на ракету будет действовать только небольшое сопротивление разреженного воздуха (направленного сверху вниз), создающего незначительную силу веса, направленную к потолку, который в этом случае станет «низом» (рис. 67, в). При запуске двигателя второй ступени снова появится нормальное ощущение тяжести, увеличивающееся стечением времени (рис. 67, г). При управлении ракетой, например при ее повороте, тяга двигателя будет некоторое время направлена в сторону. Соответственно повернется и направление силы веса (рис. 67, д).

При движении ракеты с работающими двигателями по траектории, наклоненной к Земле (рис. 67, е), ощущение тяжести по-прежнему будет нормальным, т. е она будет направлена к полу кабины, а земная поверхность покажется наклонной. С момента отключения двигателей (рис. 67, ж), если ракета будет находиться достаточно высоко и сопротивление среды будет отсутствовать, внезапно наступит состояние невесомости. Такое состояние будет продолжаться до тех пор, пока снова не заработают двигатели или ракета не встретит сопротивления атмосферы при приближении к Земле.

Если ракета запускается в не очень высокие слои атмосферы, то какая-то небольшая сила сопротивления среды останется. Благодаря ей все тела, свободно плававшие в кабине в условиях полной невесомости, станут медленно двигаться к стенке, направленной по движению ракеты, и слабо к ней прижиматься. Под действием даже незначительного сопротивления высота полета ракеты будет постепенно уменьшаться, а траектория движения походить на спираль, все круче и круче склоняющуюся к земной поверхности (рис. 68).

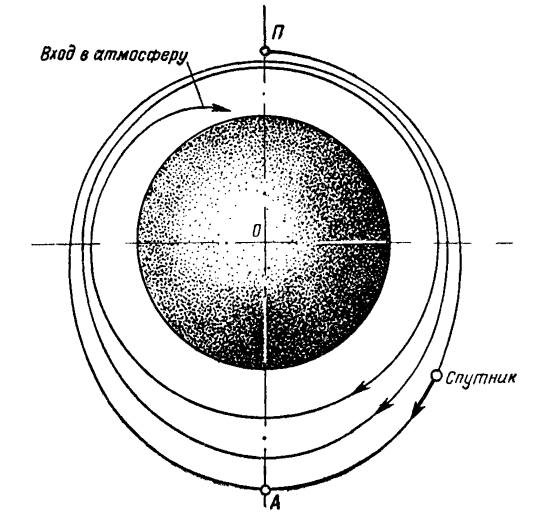
Рис. 68. Изменение формы орбиты ракеты по времени: П — начальное положение перигея орбиты; А — начальное положение апогея орбиты

При подходе к сравнительно плотным слоям атмосферы (ниже 50 км от поверхности Земли) произойдет резкое нарастание сопротивления движению. Если ракета будет двигаться к Земле носовой частью (рис. 67, з), то сопротивление воздуха Q создаст ощущение силы тяжести, направленной «вверх» по отношению к ракете, т. е. к ее потолку.