Спин фотона и электрона

Понятие спин в квантовой физике характеризует вращение частиц. Мы уже показали, что энергия фотона 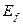и энергия 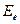свободного электрона, определяются по идентичным формулам:

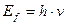, (181)

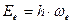. (182)

Частота колебаний, обозначаемая символом 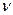, - широко используется в физике. Принято считать, что это - скалярная величина, которая легко регистрируется современными осциллографами при электрических измерениях. Константа Планка 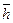- величина векторная. С учетом этого энергия фотона 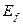, определённая по формуле (181), должна быть векторной величиной. Чтобы прояснит эту ситуацию, проанализируем физической суть частоты 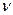. Та ли это частота, которую фиксируют осциллографы и на которой построена вся современная электродинамика? Ведь осциллограф фиксирует частоту импульсов совокупности фотонов (рис. 11), но не частоту, управляющую движением каждого фотона в отдельности (рис. 15, 16) поэтому нет оснований считать энергию фотона векторной величиной. Чтобы убедиться в этом, проанализируем связь между, как считается, скалярной 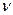частотой и угловой частотой 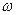, которую принято считать векторной величиной. Эта связь отражена в зависимости 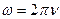, из которой следует, что если угловую частоту 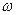рассматривать как векторную величину, то линейная частота 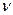- тоже величина векторная. 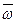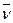Причём, направления векторов и совпадают (рис. 46).

С учетом изложенного правые части формул (181) и (182) можно рассматривать и как скалярные произведения и как векторные произведения двух векторов.

Скалярное произведение двух векторов равно произведению их модулей на косинус угла между ними. Поскольку эти векторы совпадают по направлению, то угол между ними равен нулю (рис. 46), а косинус этого угла - единице. В этом случае скалярное произведение этих векторов 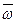и 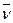равно скалярной величине и тогда энергии единичных фотонов (181) и электронов (182) – величины скалярные.

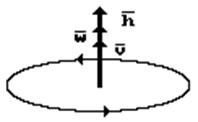
Рис. 46. Схема направления векторов 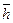, 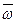и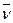

Если же рассматривать векторное произведение указанных векторов, то оно равно третьему вектору, модуль которого определяется как произведение модулей этих векторов на синус угла между ними. Поскольку синус нуля равен нулю, то векторное произведение этих векторов равно нулю и энергии единичных фотонов (181) и единичных электронов (182) также оказываются равными нулю. Из этого следует, что величины энергий единичных фотонов и единичных электронов не могут быть векторными величинами.

Если такой подход считать корректным, то снимаются мощные ограничения на процессы излучения и поглощения фотонов электронами, возникающие при векторных свойствах энергий единичных фотонов и электронов. Поэтому мы считаем изложенный анализ корректным, а энергии единичных фотонов и электронов – скалярными величинами.