Систематические погрешности, обусловленные несоответствием модели объекту.

Наиболее распространенные среди методов исключения систематических погрешностей:

• метод замещения,

• метод противопоставления,

• метод компенсации погрешности по знаку,

• метод рандомизации.

Метод измерений замещением; Метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины.

Метод измерений дополнением; метод дополнения: Метод сравнения с мерой, в котором значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению.

Метод противопоставления:

Измерение выполняется дважды и таким образом, чтобы в каждом случае причина постоянной погрешности оказывала разные, но известные по закономерности влияния на результаты измерения. Данный метод применяется тогда, когда погрешности в зависимости от условий измерения могут входить в результат с противоположными знаками.

Метод рандомизации:

Перевод систематических погрешностей инструмента в разряд случайных. Происходит измерение ФВ несколькими однотипными приборами. Для одного прибора существует систематическая погрешность. А для нескольких приборов она изменяется случайным образом. В результате: систематические погрешности присущие каждому прибору компенсируются.

ПРИМЕРЫ МЕТОДОВ РАЗОБРАТЬ САМОСТОЯТЕЛЬНО И ВПИСАТЬ В ТЕКСТ!

Причины НСП и способы их суммирования.

Систематические погрешности результата измерений оцениваются, как правило, по ее составляющим, т. е. являются составной. В зависимости от вида измерений исходных данных, суммарная погрешность оценивается по следующим формулам:

Для прямых измерениях и независимых составляющихкоторые подчиняются нормальному закону распределения (при Р=1) - алгебраическую сумму составляющих:

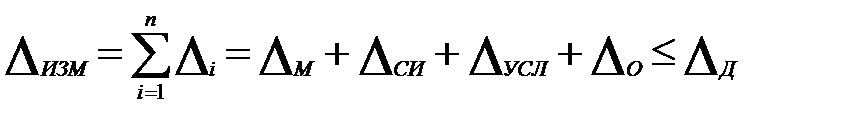
При прямых измерениях и независимых составляющих, подчинённых нормальному закону и P<1, формула:

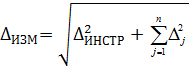
где Δинстр - инструментальная составляющая погрешности измерений (рассчитывается в зависимости от реальных условий эксплуатации СИ по формулам модели 1); Σ - объединение составляющих погрешности измерений, обусловленных методическими погрешностями, квалификацией оператора, алгоритмом обработки результатов и т. д.

При прямых измерениях и независимых суммируемых составляющих погрешностей, но при законе распределений, хотя бы для одной из суммируемых погрешностей, отличным от нормального (при Р < 1)

,

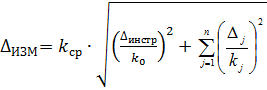где k0 и ki - коэффициент перехода Δи и Δj к соответствующим средним квадратическим отклонениям с учетом закона распределения;

kср. - коэффициент перехода от суммарного значения среднего квадратического отклонения к суммарной предельной абсолютной погрешности.

При прямых измерениях, различных законах распределения суммируемых погрешностей и наличии корреляционных связей между всеми или некоторыми из суммируемых погрешностей (при Р<1):

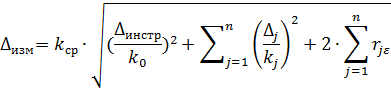
где 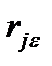- корреляционные моменты.

При косвенных измерениях, когда параметр А = f(а1, а2, а3, ... ап) функционально связан с п измеряемыми прямым способом параметрами а1, а2, а3, ... ап (при Р < 1):

,

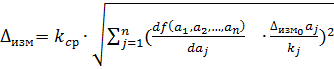где Δизм ai,- - погрешность измерений прямым способом а--го параметра, определяемая по одной из вышеприведенных формул.