Выбор числа измерений.

Определяется требованием по точности результата измерения. Увеличение числа измерения в 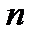раз даёт возможность уменьшить случайную погрешность в 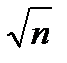раз. Систематическая погрешность уменьшается введением поправок. Погрешность поправок, не поддающаяся исключению, составляет НСП и, следовательно, случайную погрешность имеет смысл уменьшать не бесконечно, а до определённого значения, зависящего от границ НСП.

Рассмотрим задачу рационального выбора числа измерения n в зависимости от соотношения НСП и случайной погрешности. При однократном измерении погрешность вычисляется по формуле

,

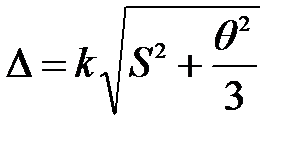где k-поправочный коэффициент, зависящий от принятой доверительной вероятности Р и от вида распределения суммарной погрешности.

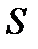- СКО, 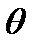-граница НСП.

В случае, если 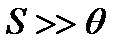, целесообразно выполнять многократные измерения, чтобы… В этом случае суммарная погрешность будет определяться по формуле

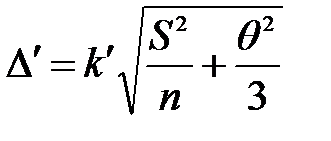
k – коэффициент, зависящий от Р и распределения суммарной погрешности

При 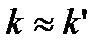- по формуле

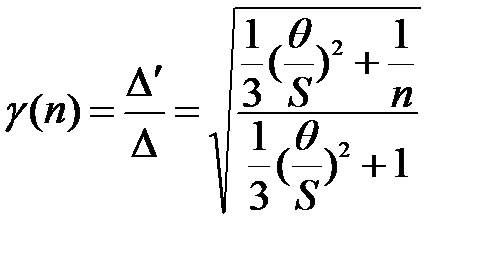
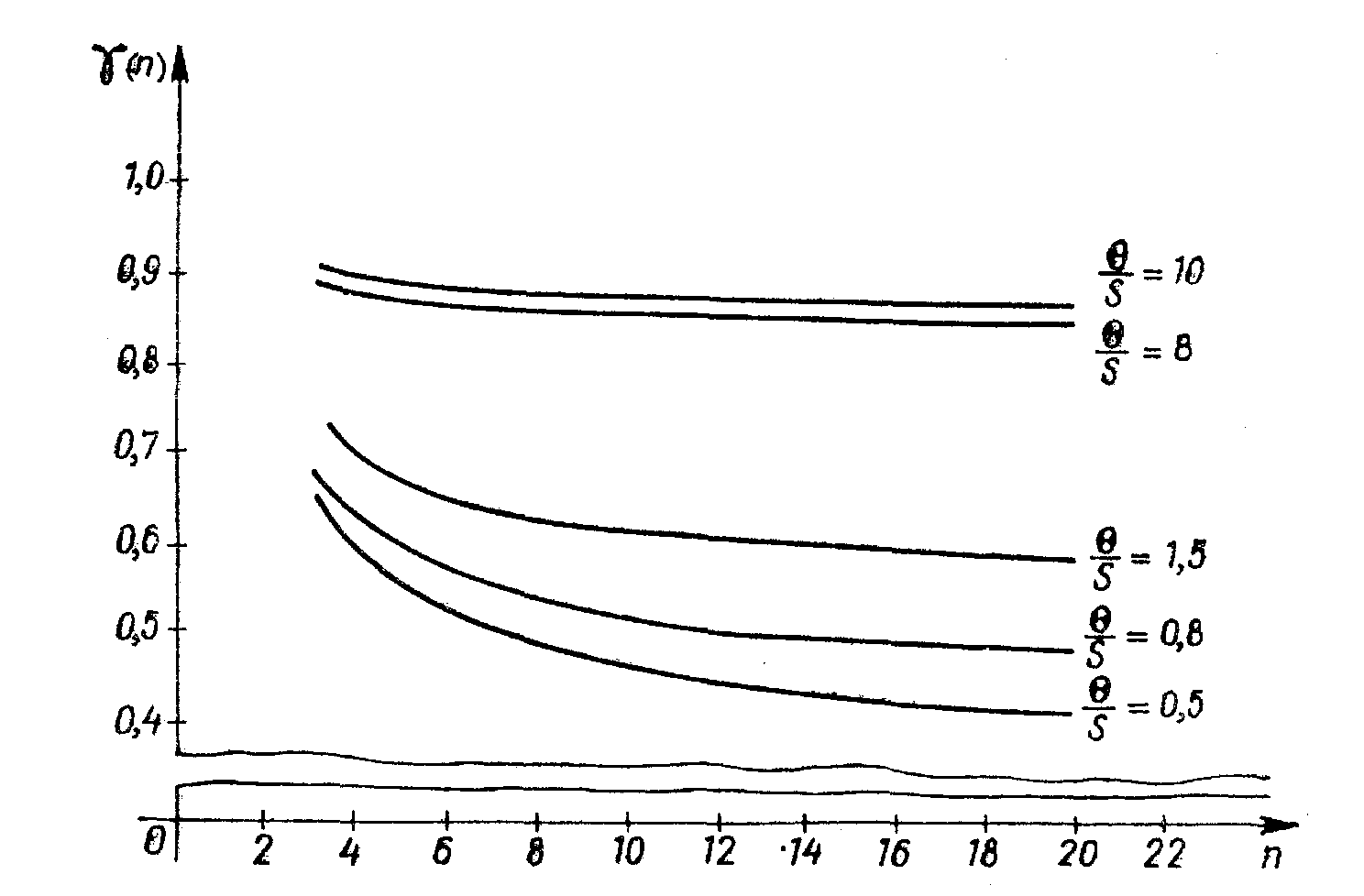
Строим зависимости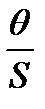

Если 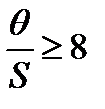, то мы видим, что по существу эта зависимость горизонтальная, то есть не зависит от n. При 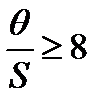нет смысла в многократных измерениях, так как погрешность не уменьшается, а затраты увеличиваются.

Если 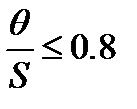, то существенную роль в результате играют случайные погрешности, следовательно, целесообразно проводить многократные измерения, но не бесконечно. Если 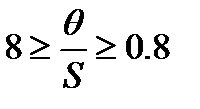, необходимо учитывать и случайные погрешности, и НСП, а по углу наклона решать вопрос о количестве измерений.