Приток жидкости к несовершенным скважинам. Виды несовершенства скважин. Приведенный радиус скважин
Скважина называется гидродинамически совершенной, если она вскрывает продуктивный пласт на всю толщину и забой скважины открытый, т.е. вся вскрытая поверхность забоя является фильтрующей. Однако во многих случаях продуктивные пласты вскрываются скважинами не на всю их толщину, а частично; такие скважины считаются несовершенными.
В подземной гидрогазодинамике различают два основных вида несовершенства скважины (рис. 28):
1) гидродинамически несовершенная по степени вскрытия продуктивного пласта;
2) гидродинамически несовершенная по характеру вскрытия пласта.
Скважина называется гидродинамически несовершенной по степени вскрытия пласта, если она вскрывает пласт не на всю толщину h пласта, а только на некоторую ее глубину b с открытым забоем; при этом отношение b/h=h (h с чертой сверху) называется относительным вскрытием пласта.
Скважина называется гидродинамически несовершенной по характеру вскрытия пласта, если она вскрывает весь пласт (до подошвы), но сообщение с пластом происходит через специальные отверстия в обсадной колонне и цементном камне или через специальные забойные фильтры.
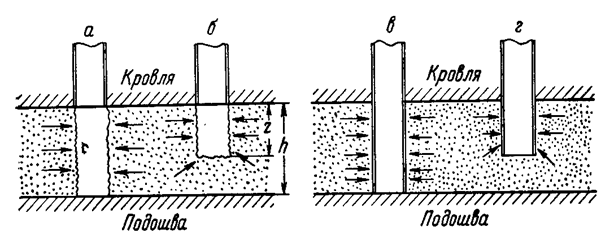
Схема гидродинамически совершенной и несовершенных скважин
а- гидродинамически совершенная скважина; б- скважина, не совершенная по степени вскрытия; в- скважина, не совершенная по характеру вскрытия; г- скважина, не совершенная по характеру и степени вскрытия.
Нередко встречаются скважины с двойным видом несовершенства – как по степени, так и по характеру вскрытия пласта.
Приток жидкости к несовершенным скважинам даже в горизонтальном однородном пласте постоянной толщины перестает быть плоско-радиальным. Строгое математическое решение задачи о притоке жидкости к несовершенной скважине в пластах конечной толщины представляет большие (иногда непреодолимые) математические трудности. Приведем без выводов и доказательств несколько известных решений по определению дебита несовершенной по степени вскрытия скважины.
Прежде всего допустим, что скважина вскрыла кровлю пласта неограниченной толщины (h →∞) и при этом ее забой имеет форму полусферы. В этом случае можно считать, что поток радиально-сферический при условии RК→∞ .
Если скважина вскрыла пласт неограниченной толщины на глубину b, то ее дебит можно найти по формуле Н.К. Гиринского:
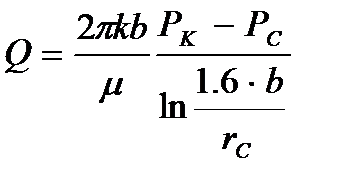
Подбирая интенсивность расходов q и используя метод суперпозиции действительных и отображенных стоков, М.Маскет получил следующую формулу для дебита гидродинамически несовершенной скважины:
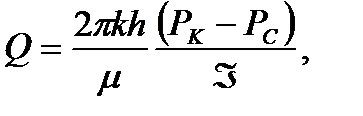
Иногда для расчета дебита несовершенной скважины используется бо-лее простая формула И. Козени
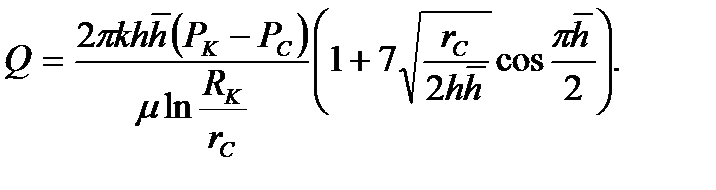
При расчете несовершенных скважин нередко используют понятие приведенного радиуса несовершенной скважины
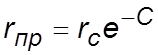
где rC– радиус совершенной скважины, С – коэффициент несовершен-ства.
Приведенный радиус – это радиус такой совершенной скважины, дебит которой равняется дебиту данной несовершенной скважины при тех же условиях эксплуатации.
Таким образом, вначале находятся приведённые радиусы rпр и дальней-ший расчет несовершенных скважин ведется как для совершенных скважин радиуса rпр.
Таким образом, дебит несовершенной скважины можно определить, если известен параметр несовершенства или приведённый радиус rпр , а также известна соответствующая формула дебита совершенной скважины. Влияние несовершенства скважины на приток при существовании закона фильтрации Дарси можно учесть величиной коэффициента С, основываясь на электрической аналогии. Согласно данной аналогии различие в дебитах совершенной и несовершенной скважин объясняется наличием добавочного фильтрационного сопротивления несовершенной скважины, т.е. дебит несовершенной скважины можно представить в виде:
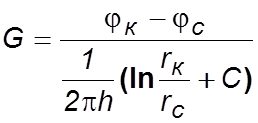
Дата добавления: 2018-05-25; просмотров: 2800;











