Особенности фильтрации неньютоновских жидкостей
Классификация неньютоновских жидкостей.
Особенности фильтрации неньютоновских нефтей связаны с повышенным содержанием высокомолекулярных компонентов – смол, асфальтенов, парафина.
Классификация неньютоновских жидкостей обычно основывается на виде зависимости скорости сдвига g ’= dv / dr от величины касательного напряжения t.
Все неньютоновские жидкости могут быть разбиты на три класса:
1. Системы, для которых скорость сдвига зависит только от величины касательного напряжения, т.е dv / dr = f (t ), - неньютоновские вязкие жидкости.
2. Системы, для которых скорость сдвига зависит как от величины касательного напряжения, так и от времени dv / dr = f (t ,t). Если с течением времени при заданной величине g ’ напряжение уменьшается, то жидкость называется тиксотропной, а если возрастает – реопектической.
3. Системы, обладающие свойствами как твердого тела, так и жидкости и частично проявляющие упругое восстановление формы после снятия напряжения – вязкоупругие.
Тиксотропия - специфическое свойство коагуляционных структур. Разрушение структуры выражается в разрыве контактов между частицами дисперсной фазы, а ее тиксотропное восстановление - в возобновлении этих контактов вследствие подвижности среды и броуновского движения частиц. Неньютоновские вязкие жидкости в свою очередь могут быть разделены на две группы:
а) жидкости, обладающие начальным напряжением сдвига t0, то есть жидкости, которые начинают течь лишь после того, как касательное напряжение превысит некоторый предел t;
б) жидкости, не обладающие начальным напряжением сдвига. Примером жидкости с начальным напряжением сдвига является вязкопластичная жидкость, или жидкость Бингама-Шведова. Ее реологическое уравнение имеет вид
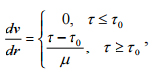
где t-начальное напряжение сдвига, m - коэффициент пластической вязкости.
Модель вязкопластичной жидкости широко используется при описании поведения глинистых растворов, буровых шламов и т.п.
Важный эффект фильтрации с предельным градиентом давления – возможность образования в пласте застойных зон, где движение нефти отсутствует. Эти зоны образуются в тех участках пласта, где градиент давления меньше предельного.
Показано, что для получения качественных результатов при моделировании фильтрации сложных сред необходимо учитывать эффекты релаксации. При этом течение жидкости осуществляется по закону фильтрации, имеющему неравновесный характер, например 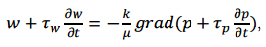
где tw и tр – время релаксации скорости фильтрации и давления
Для ньютоновской жидкости единственным параметром, характеризующим ее течение, служит коэффициент динамической вязкости - коэффициент пропорциональности в законе вязкого трения Ньютона: 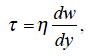 (1)
(1)
где τ - касательное напряжение сдвига: dw/dy - градиент скорости в направлении, перпендикулярном направлению течения х.
Зависимость τ от dw/dy выражается в этом случае прямой линией, проходящей через начало координат.
Жидкости, не подчиняющиеся закону трения (1). называются аномальными или неньютоновскими. Неньютоновские жидкости подразделяются на три класса.
1. Неньютоновские вязкие жидкости, для которых касательное напряжение зависит только от градиента скорости (стационарно реологические жидкости): 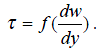 (2)
(2)
2. Жидкости, для которых связь между τ и dw/dy зависит от времени действия напряжений (нестационарно реологические жидкости):
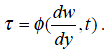
3. Вязкоупругие жидкости, т.е. среды, обладающие свойствами как твердого тела, так и жидкости, а также способные к частичному восстановлению формы после снятия напряжений. Для таких сред зависимость между касательными напряжениями и градиентом скорости значительно сложнее она включает производные по времени как напряжений, так и градиента скорости.
Среди неньютоновских жидкостей первого класса, описываемых уравнением (2). можно выделить три типа.
А. Вязкопластичные жидкости, для которых уравнение (2) имеет следующий вид:
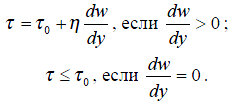 (3)
(3)
Графическое представление этой зависимости называется реологической кривой (или кривой течения). В равенство (3). кроме коэффициента вязкости η входит также постоянная τ0 называемая начальным (или предельным) напряжением сдвига. Считается, что при τ<τ0 жидкость ведет себя как твердое тело, и течение отсутствует. Это объясняется наличием у покоящейся вязко-пластичной жидкости пространственной жесткой структуры, сопротивляющейся любому напряжению τ меньшему τ0. Когда τ становится больше τ0. структура полностью разрушается, и жидкость ведет себя как ньютоновская среда (при этом «пластические» и «вязкие» напряжения складываются). Если τ уменьшается до значения τ0. то структура опять восстанавливается.
Б. Псевдопластичные жидкости. Эксперименты показали, что для таких сред связь между напряжением сдвига и градиентом скорости в логарифмических координатах оказывается на некотором участке линейной. Угловой коэффициент соответствующей прямой заключен между О и 1. Поэтому для описания таких сред предложена степенная зависимость:
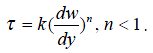 (4)
(4)
где k и n - постоянные для данной жидкости: коэффициент k - мера консистенции жидкости, которая увеличивается с возрастанием вязкости: показатель n характеризует степень отклонения данной жидкости от ньютоновской.
Модель псевдопластичной жидкости применяется, в частности, для описания растворов и расплавов полимеров.
Введем понятия кажущейся вязкости η* как отношение касательного напряжения к градиенту скорости:
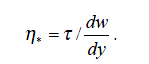
В. Дилатантные жидкости описываются степенным уравнением (4). но при n > 1. У этих жидкостей кажущаяся вязкость η*. увеличивается с возрастанием градиента скорости. Модель дилатантной жидкости хорошо описывает поведение суспензий с большим содержанием твердой фазы.
Рассмотрим наиболее простой случай течения среды с неньютонов- скими свойствами, стационарное движение вязкопластичной жидкости (3) в одной поре как в капиллярной трубке постоянного радиуса. На некотором расстоянии r0 от оси трубки касательное напряжение τ = τ0. что выражается равенством (3). где dw/dy=dw/dr. причем dw/dr=0 при r=r0 .
Движение аномальных нефтей в пластах по закону фильтрации вязкопластической жидкости пористой среде приводит к существенным особенностям разработки этих пластов не встречающихся случае фильтрации по закону Дарси.
Рассмотрим плоскорадиальный приток несжимаемой вязкопластичной жидкости (ВПЖ) скважине:
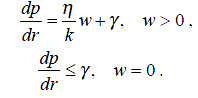
Выведем формулу для дебита скважины в круговом пласте, обобщающую формулу Дюпюи:
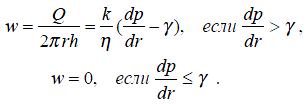
Считая заданными постоянные давления на забое скважины и на границе пласта
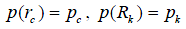
(pk>pc) для рассматриваемого случая притока и pk<pc при закачке жидкости в пласт, после интегрирования находим
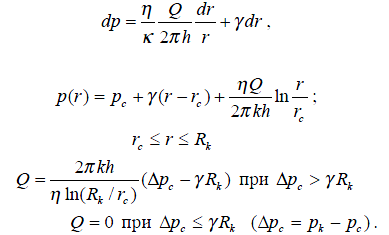
Формулами соответственно представлены распределения давления в пласте и дебит скважины. Из формул видно, что часть разности давлений в линейного слагаемого с угловым коэффициентом γ (предельный градиент давления) теряется на преодоление градиента давления сдвига. Как видно наличие предельного градиента давления в пласте ведет к уменьшению дебита скважины при тех же условиях по сравнению с фильтрацией по закону Дарси (формула Дюпюи).
В случае слоистого пласта с гидродинамически изолированными пропластками, т.е. в отсутствие перетоков между слоями с разными проницаемостями. Формула для дебита в каждом пропластке:
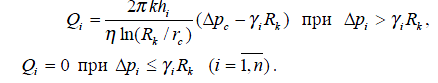
Суммарный дебит равен: 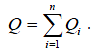
Дата добавления: 2018-05-25; просмотров: 2544;











