Теоретические основы анализа результатов прогнозирования спроса на товарных рынках

После проведения прогнозных расчетов, необходима верификация прогнозов. Помимо абсолютной верификации (эмпирическое подтверждение данных прогноза) существует относительная. Абсолютная верификация возможна только после перехода периода упреждения из будущего в прошлое. Но задолго до этого можно проводить параллельное или повторное исследование по этой методике (например, провести опрос экспертов). Если результаты совпадают, то есть основание считать степень достоверности прогноза высокой. Если нет, то есть время для поиска и устранения ошибок в методике разработки прогноза. Следовательно, необходимо различать достоверность (обоснованность) и истинность (точность) прогноза. Обоснованность характеризует уровень состояния знаний и качества научных исследований. Истинность проверяется практикой. Важнейшая характеристика прогнозов – точность.

О ней принято судить по величине погрешности (ошибки) прогноза – разности между прогнозируемым и фактическим значением исследуемой переменной. Такого рода оценки можно получить, когда период упреждения уже окончился и известны фактические значения переменной (это апостериорные оценки качества прогнозов). К ним относятся абсолютные и относительные показатели, позволяющие количественно определить величину ошибки прогноза в единицах измерения прогнозируемого объекта или в процентах.

а) абсолютная ошибка:

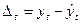
t-момент времени при котором определен показатель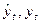

б) средняя абсолютная ошибка:

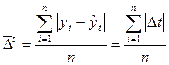
в) среднеквадратическая ошибка:

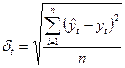
Недостатком этих показателей является то, что их значение существенно зависит от масштаба исследуемых явлений, поэтому прибегают к расчету ошибок в относительном выражении.

г) относительная ошибка прогноза:

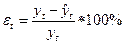
д) средняя относительная ошибка:

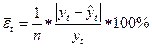
Данные показатели, как правило, используются при сравнении точности прогнозов различных объектов прогнозирования, т.к. они характеризуют относительную точность прогноза.

Высокая точность прогноза определяется процентом не больше 5. До 10% прогноз считается допустимым. Т.е. точность прогноза тем выше, чем ниже величина ошибки позволяющая сравнивать прогнозные и фактические значения исследуемой величины.

Следует отметить, что точность единичного прогноза мало что может сказать исследователю, т.к. на формирование исследуемого явления влияет множество разнообразных факторов, следовательно, полное совпадение или значительное расхождение прогноза и его реализации может быть следствием особо благоприятных или неблагоприятных обстоятельств. Единичный «хороший» прогноз может быть получен и по «плохой модели» и наоборот, следовательно, о качестве прогнозов применяемых моделей можно судить лишь о совокупности сопоставления прогнозов с их реализацией.

Наиболее простой мерой качества прогнозов при условии, что имеются данные об их реализации, может быть относительное число случаев, когда фактическая реализация охватывалась интервальным прогнозом к общему числу прогнозов, т.е.

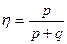
где:

p – число прогнозов, подтвержденных фактическими данным;

q – число прогнозов, не подтвержденных фактическими данными.

Когда все прогнозы подтверждаются:

q=1 и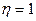

Если же все прогнозы не подтверждаются, то

p=0 и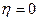

Так как ширина доверительного интервала в значительной мере зависит от принятой доверительной вероятности (чем меньше вероятность, тем уже интервал), то сопоставление коэффициентов 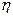для разных моделей и инструментов прогноза имеет смысл при условии, что доверительные вероятности приняты одинаковыми. Расчеты прогнозов по различным методикам для повышения достоверности полученных результатов должны быть проверены на непротиворечивость (согласованность). Если они признаны согласованными, то возможно объединение прогнозных результатов, т.е. синтез прогнозных оценок в целом построения комбинированного прогноза. Для оценки согласованности прогнозов рассматривают варианты возможного расположения доверительных интервалов. Например, для двух прогнозов экстраполяционного и экспертного возможно следующее взаимное расположение доверительных интервалов.

А.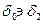

Б.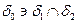

В.

Основное правило непротиворечивости прогноза: результаты их являются согласованными, если значение принадлежит общей области. На рисунке А доверительный интервал одного прогноза охватывает доверительный интервал другого. На рисунке Б имеет место пересечение интервалов. На рисунке В полное противоречие результатов.

Рассмотренные выше апостериорные оценки точности прогнозов основаны на том, что получены фактические значения величин, которые были оценены при разработке прогноза. Однако в практике проблему точности надо решать, когда период упреждения еще не пришел и истинные значения прогнозируемой переменной неизвестны. Эта проблема решается на основе получения оптимальных оценок, которые на самом деле являются оценками достоверности используемых моделей.

Априорную точность прогноза связывают с размером доверительного интервала. Модель, дающая более узкий доверительный интервал при одной и той же доверительной вероятности является более точной. Для точной оценки прогнозов используют такие характеристики как:

· Средняя и относительная ошибка.

· Средне линейное отклонение.

· Оценка стандартной ошибки.

· Корреляционные отношения.

· Критерий Фишера.

Наряду с указанными статистическими характеристиками для анализа достоверности полученной модели проводят оценку значимости параметров (проверка нулевых гипотез) и строят доверительные интервалы.

Эти и другие возможные характеристики показывают степень приближения модели к реальным наблюдениям за процессом, а чем адекватнее модель, тем выше вероятность получения с ее помощью более точного прогноза.

Проверка модели (методики прогнозирования) может осуществляться на основе так называемого ретроспективного прогноза, т.е. когда прогнозирование осуществляется для некоторого момента времени в прошлом, для которого уже имеются фактические данные. При этом существующая информация делится на две части: 1. охватывающая более ранние периоды, служит для оценивания параметров прогностической модели; 2. более поздние данные рассматриваются как реализация соответствующих прогностических оценок. Полученные ретроспективно ошибки прогноза в определенной мере характеризуют точность применяемой методики прогнозирования и могут оказаться полезными при сопоставлении нескольких методов, однако однозначные выводы о качестве прогнозов по данной методике сделать сложно, учитывая, что оценка качества прогнозов получена при использовании лишь части имеющихся данных.

Для оценки качества прогнозов имеется характеристика надежности прогноза, определяется вероятностью наступления прогнозируемого события, т.е. реализации соответствующей прогностической оценки. Чем она выше, тем выше надежность. Оценка прогноза может проводиться субъективно (экспертное прогнозирование), либо связывается с доверительными интервалами прогноза, если последний, основан на статистической модели.

Рассмотренные понятия априорной точности прогнозов могут использоваться практике, при условии содержательного обоснования используемой модели. В противном случае полученные оценки лишь создают иллюзию точности. Неточность прогнозов несмотря на ограничения налагаемые использованием аппарата математической статистики в значительной степени влияет адекватность применяемой модели, т.е. ее соответствие изучаемому явлению.

На процесс выбора модели влияет весь комплекс условий, в которых получены фактические и расчетные значения показателей:

1. стабильность социально-экономических факторов, влияющих на изучаемый объект;

2. информативность факторных признаков по отношению к результативному показателю;

3. достоверность информации;

4. репрезентативность выборки;

5. адекватность способа построения модели.

На повышение адекватности модели может повлиять ее корректировка при появлении новой информации. В этом случае корректировка является адаптацией модели изменившимися условиями ее функционирования.

Условия непротиворечивости прогнозных результатов выполнены в случае возможности реализации процедуры синтеза, сущность которой состоит в том, что определяется средневзвешенный результат прогноза, полученного различными методами с учетом их достоверности. Чем менее достоверен результат, тем меньше его вес, т. е. вклад в окончательный прогноз. Далее строится синтезирующая оценка прогноза, которой является линейная комбинация:

У = f_i * y_{i ,}

где

y_i - значение частного i – го прогноза;

f_i – вес i-го прогноза.

Таким образом получают комбинированный прогноз, который предполагает синтез прогнозов.