Математическое описание свободных частиц

В большинстве экспериментов элементарные частицы в начальной и конечной стадиях являются свободными, двигаясь в камере Вильсона, пузырьковой камере или эмульсии и при этом, возможно, взаимодействуя с внешним электрическим или магнитным полем. Поэтому математическое описание явлений естественно начать с рассмотрения свободных частиц. Для этой цели достаточны хорошо известные методы обычной линейной теории поля. Каждому виду элементарных частиц сопоставляется полевой оператор ψ_α(х), удовлетворяющий линейному дифференциальному уравнению

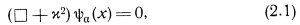
где ϰ — масса частицы, х — пространственно-временные координаты. Индекс α используется для характеристики трансформационных свойств частицы по отношению к различным группам преобразований и тем самым для указания ее спина, изоспина и других квантовых чисел. Точно так же х можно рассматривать просто как непрерывный параметр, необходимый для определения трансформационных свойств относительно неоднородной части группы Лоренца, т. е. подгруппы трансляций. Математически состояния свободных частиц можно в известном смысле рассматривать как некоторые представления групп, лежащих в основе теории. Тогда состояние свободной частицы можно выразить, применяя к вакуумному состоянию полевой оператор ψ_α(x):

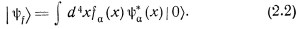
Здесь числитель дроби с_αβ(р) зависит от рассматриваемого представления. Правую часть равенства (2.4) удобно интегрировать по р₁ р₂ и р₃ вдоль вещественных осей, но в комплексной р_о-плоскости контур интегрирования надо выбирать в зависимости от упорядоченности сомножителей, стоящих в левой части. Для разных типов упорядоченности (например, для хронологического произведения, для коммутатора или антикоммутатора) необходимы различные контуры интегрирования. Подробности о соотношениях, при которых существенно наличие полюса в точке р² — ϰ² = 0, можно найти в книгах по квантовой теории поля. Соответствующие результаты кратко суммированы в приложении I.

Когда частицы движутся под действием внешнего электромагнитного поля, их поведение можно описать линейным волновым уравнением, которое отличается от (2.1) некоторыми дополнительными членами, зависящими от заряда, магнитного момента и других электромагнитных свойств частиц.

Таким образом, все множество различных полевых операторов для разных типов свободных частиц (и соответствующие им волновые уравнения) содержит большое количество важной информации о свойствах частиц. Они пригодны для характеристики ситуации в начале и конце эксперимента. Поэтому часто их называют in или out операторами или асимптотическими операторами.

С другой стороны, как математический аппарат при формулировке теории элементарных частиц эти операторы не очень полезны. Они являются вторичными величинами, выводимыми из асимптотического поведения других выражений, которые более фундаментальны и которые описывают внутренние механизмы мира элементарных частиц. Асимптотические операторы можно построить лишь после того, как найдено решение математических проблем физики элементарных частиц.

Начальное или конечное состояния являются по определению такими состояниями, в которых взаимодействием между частицами можно пренебречь. Действуя на вакуум полиномами из асимптотических операторов, можно построить такие и только такие состояния. Обычно предполагается, что они образуют полный набор; это значит, что любое взаимодействие в итоге, когда оно становится пренебрежимо малым, приводит систему к состоянию из этого же набора. Но даже если это так, сами состояния взаимодействия могут принадлежать к более широкой совокупности, которую нельзя представить только асимптотическими состояниями.

Кроме того, идея о полноте набора асимптотических состояний сталкивается с трудностью: любое из них, как правило, содержит неизвестное число ненаблюдаемых инфракрасных световых квантов. Поэтому истинное состояние является не «чистым» (в квантово-механическом смысле), а скорее «смешанным». Однако эти трудности имеют более формальную природу, и мы не будем обсуждать их детально. Во многих случаях влияние инфракрасных квантов несущественно, и им можно просто пренебречь.