Вычисление НОД. Алгоритм Евклида
Алгоритм Евклида дает возможность вычислить наибольший общий делитель для любых двух целых чисел. Для описания алгоритма рассмотрим следующие две леммы.
Лемма 1. Если 

 , то
, то 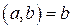 .
.
Доказательство. Очевидно, что  – общий делитель чисел
– общий делитель чисел  и
и  , поскольку
, поскольку 

 и
и 

 . Пусть
. Пусть  – общий делитель чисел
– общий делитель чисел  и
и  , тогда
, тогда 

 . Значит,
. Значит,  – наибольший общий делитель чисел
– наибольший общий делитель чисел  и
и  по определению.
по определению.
Лемма 2. Пусть 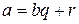 , причем числа
, причем числа 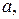
 и
и 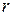 отличны от 0 и
отличны от 0 и 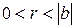 . Тогда
. Тогда 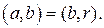
Доказательство. Пусть  множество общих делителей чисел
множество общих делителей чисел  и
и  , а
, а 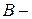 множество общих делителей чисел
множество общих делителей чисел  и
и 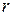 . Докажем, что
. Докажем, что 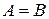 .
.
Пусть 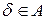 , это значит, что
, это значит, что 

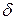 и
и 

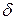 . Тогда по свойству делимости
. Тогда по свойству делимости 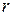

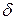 . Тогда,
. Тогда, 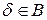 , следовательно,
, следовательно, 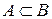 . Аналогично докажем, что
. Аналогично докажем, что 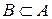 . Из определения равенства двух множеств получим, что
. Из определения равенства двух множеств получим, что 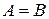 .
.
Если два числовых множества совпадают, то совпадают их наибольшие по величине элементы, что и доказывает лемму.
Сформулируем теперь алгоритм Евклида.
Рассмотрим два целых числа  и
и  . Пусть
. Пусть 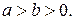 Требуется найти наибольший общий делитель чисел
Требуется найти наибольший общий делитель чисел  и
и  .
.
Шаг 1. Разделим  на
на  . Если
. Если 

 , то по лемме 1 получим, что
, то по лемме 1 получим, что 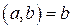 .
.
Если число  не делится на
не делится на  , то
, то 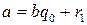 , где
, где 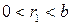 . Тогда по лемме 2
. Тогда по лемме 2 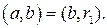
Шаг 2. Разделим  на
на 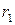 . Если
. Если 

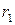 , то
, то 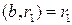 (по лемме 1). Тогда
(по лемме 1). Тогда 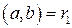 .
.
Если  не делится на
не делится на 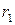 , то
, то 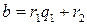 , где
, где 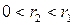 . Тогда по лемме 2
. Тогда по лемме 2 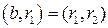 , а значит, справедливо и
, а значит, справедливо и 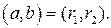
Продолжая процесс деления, получим последовательность остатков – убывающую последовательность целых неотрицательных чисел, вычисляемых по следующим рекуррентным формулам: 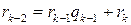 .
.
Поскольку такая последовательность не может иметь бесконечно много членов, на некотором шаге очередной остаток окажется равным нулю. Тогда последний, отличный от нуля остаток и есть НОД чисел  и
и  .
.
Пример. Найдем НОД чисел 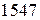 и
и 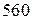 . Для этого разделим
. Для этого разделим 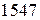 на
на 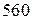 , получим
, получим 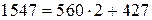 . Таким образом, первый полученный остаток
. Таким образом, первый полученный остаток 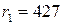 .
.
Далее, разделим 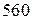 на
на 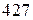 , получим
, получим  , при этом
, при этом 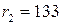 . Продолжим процесс деления:
. Продолжим процесс деления:
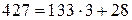 ,
, 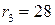 ;
;
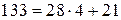 ,
, 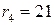 ;
;
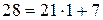 ,
, 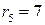 ;
;
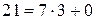 ,
, 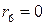 .
.
Таким образом, последний отличный от 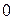 остаток равен
остаток равен  , это и есть наибольший общий делитель чисел
, это и есть наибольший общий делитель чисел 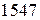 и
и 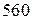 .
.
В следующей теореме утверждается, что наибольший общий делитель двух чисел можно представить в виде линейной комбинации этих чисел с целыми коэффициентами.
Теорема 4.1. (линейное представление НОД )
Рассмотрим два целых числа  и
и  . Пусть
. Пусть 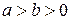 ,
, 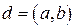 . Тогда найдутся такие целые числа
. Тогда найдутся такие целые числа 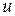 и
и 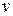 , что
, что 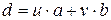 .
.
Доказательство. Докажем, что каждый из остатков  , полученных в процессе выполнения алгоритма Евклида, можно представить в виде линейной комбинации чисел
, полученных в процессе выполнения алгоритма Евклида, можно представить в виде линейной комбинации чисел  и
и  с целыми коэффициентами. Тогда это утверждение будет справедливо в частности и для последнего, отличного от
с целыми коэффициентами. Тогда это утверждение будет справедливо в частности и для последнего, отличного от 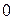 остатка, равного
остатка, равного 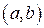 . Будем доказывать это утверждение методом математической индукции.
. Будем доказывать это утверждение методом математической индукции.
База индукции.
Пусть 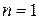 . Имеем
. Имеем 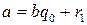 , тогда
, тогда 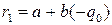 . Получили, что остаток
. Получили, что остаток 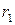 можно представить в виде линейной комбинации чисел
можно представить в виде линейной комбинации чисел  и
и  с целыми коэффициентами
с целыми коэффициентами 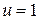 и
и 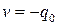 .
.
Индукционный переход.
Пусть утверждение справедливо для всех натуральных чисел 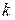 , не превосходящих
, не превосходящих 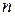 :
: 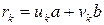 , при
, при 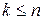 . Докажем, что это утверждение справедливо также для
. Докажем, что это утверждение справедливо также для 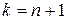 .
.
Из алгоритма Евклида следует, что
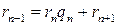
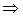
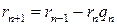 .
.
По индукционному предположению
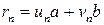 и
и 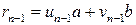 .
.
Следовательно, 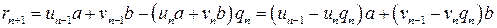 .
.
Положим 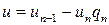 и
и 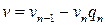 . Тогда
. Тогда 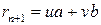 , что и требовалось установить.
, что и требовалось установить.
Пример. В предыдущем примере был найден НОД чисел 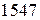 и
и 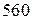 :
:  . Найдем его линейное представление:
. Найдем его линейное представление:
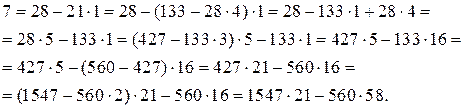
Итак, получили, что 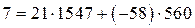 , т. е. представили НОД чисел
, т. е. представили НОД чисел 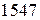 и
и 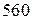 в виде их линейной комбинации с целыми коэффициентами.
в виде их линейной комбинации с целыми коэффициентами.
Дата добавления: 2021-02-19; просмотров: 490;











