ДЕЛИМОСТЬ ЧИСЕЛ. ДЕЛЕНИЕ С ОСТАТКОМ. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ.
Известно, что сумма, разность и произведение целых чисел является целым числом. Этот факт принято называть замкнутостью множества целых чисел по отношению к действиям сложения, вычитания и умножения. По отношению к действию деления множество целых чисел, очевидно, замкнутым не является. Например, результат деления числа 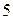 на число
на число 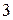 целым не является. Однако в некоторых случаях результат деления целого числа на целое число также является целым. Введем следующее определение.
целым не является. Однако в некоторых случаях результат деления целого числа на целое число также является целым. Введем следующее определение.
Определение 1.1. Пусть  и
и  – целые числа. Говорят, что число
– целые числа. Говорят, что число  делится на число
делится на число  , если найдется такое целое число
, если найдется такое целое число  , что
, что 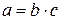 . При этом число
. При этом число  называют делимым, число
называют делимым, число  – делителем, а число
– делителем, а число  – частным.
– частным.
Факт делимости числа  на число
на число  обозначают
обозначают 

 . Также говорят, что
. Также говорят, что  кратно
кратно  .
.
Примеры. 1) 65  13, так как
13, так как 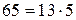 ;
;
2) 0  3, так как
3, так как 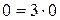 ;
;
3) 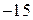
 5, так как
5, так как 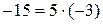 .
.

 В определении делимости ничего не говорится о том, сколько различных значений может иметь частное от деления
В определении делимости ничего не говорится о том, сколько различных значений может иметь частное от деления  на
на  . Предположим, что при делении
. Предположим, что при делении  на
на  могут быть различные частные. Это значит, что существуют такие различные целые числа
могут быть различные частные. Это значит, что существуют такие различные целые числа  и
и  , что выполняются равенства
, что выполняются равенства 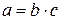 и
и 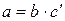 . Тогда
. Тогда
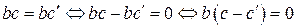 .
.
Если  , то
, то 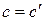 . Значит, в случае, когда делитель отличен от нуля, частное единственно.
. Значит, в случае, когда делитель отличен от нуля, частное единственно.
Если 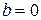 , то, очевидно,
, то, очевидно, 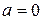 , и равенство
, и равенство 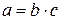 выполняется для любого значения
выполняется для любого значения  .Таким образом, на
.Таким образом, на 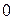 делится только
делится только 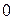 , а частное от такого деления неопределенно (может быть любым числом).
, а частное от такого деления неопределенно (может быть любым числом).
В дальнейшем, говоря о делении, всегда будем предполагать, что делитель отличен от 0.
Свойства делимости
1. Если 

 , то
, то 
 (–
(–  ); (–
); (–  )
) 
 ; (–
; (–  )
) 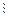 (–
(–  ).
).
Доказательство. Пусть 

 , это значит, что существует такое целое число
, это значит, что существует такое целое число  , что
, что 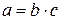 . Тогда
. Тогда 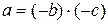 , причем число
, причем число 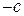 также является целым. Следовательно, по определению делимости
также является целым. Следовательно, по определению делимости 
 (–
(–  ). Остальные утверждения доказываются аналогично.
). Остальные утверждения доказываются аналогично.
2. Если 

 и
и 

 , то
, то 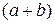

 .
.
Доказательство. 


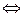
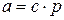 , где
, где 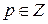 ;
; 


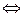
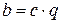 , где
, где  . Тогда
. Тогда 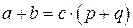 . Число
. Число 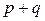 – целое, значит,
– целое, значит, 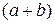

 .
.
Следствие. Из свойств 1 и 2 непосредственно следует, что если 

 и
и 

 , то
, то 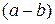

 .
.
3. Если 

 и
и 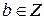 , то
, то 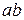

 .
.
Доказательство. 


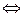
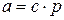 , где
, где 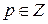 . Умножим обе части последнего равенства на
. Умножим обе части последнего равенства на  , получим
, получим 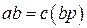 . Число
. Число  – целое, значит,
– целое, значит, 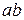

 .
.
4. Если 

 и
и  не делится на
не делится на  , то
, то 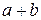 не делится на
не делится на  .
.
Доказательство. Предположим, что данное утверждение неверно: 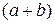

 . Это значит, что
. Это значит, что 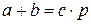 , где
, где 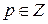 . Тогда
. Тогда 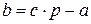 . Но
. Но 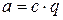 , где
, где  . Следовательно,
. Следовательно, 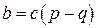 . Поскольку
. Поскольку 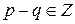 , получим, что
, получим, что 

 , что противоречит условию. Полученное противоречие доказывает, что сделанное нами предположение неверно.
, что противоречит условию. Полученное противоречие доказывает, что сделанное нами предположение неверно.
5. Если  и
и 

 , то
, то 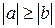 .
.
Доказательство. 


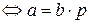 , где
, где 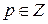 , причем
, причем 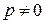 . Тогда
. Тогда 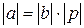 . Но
. Но 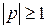 , значит
, значит 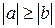 .
.
Следствие 1. Если 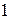

 , то либо
, то либо  , либо
, либо 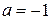 .
.
Доказательство. Если 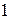

 , то по свойству 5 справедливо неравенство
, то по свойству 5 справедливо неравенство 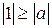 . При этом
. При этом  – целое число, отличное от 0. Следовательно,
– целое число, отличное от 0. Следовательно, 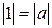 , а это и значит, что либо
, а это и значит, что либо  , либо
, либо 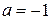 .
.
Следствие 2. Если 

 и
и 

 , то либо
, то либо 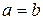 , либо
, либо  .
.
Доказательство. Если 

 и
и 

 , то по свойству 5 справедливы неравенства
, то по свойству 5 справедливы неравенства 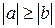 и
и 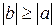 . Одновременное выполнение этих неравенств может быть только в случае, когда
. Одновременное выполнение этих неравенств может быть только в случае, когда 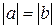 , что и означает, что либо
, что и означает, что либо 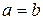 , либо
, либо  .
.
Отметим, что отношение делимости является бинарным отношением на множестве 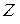 . Рассмотрим его свойства делимости как бинарного отношения.
. Рассмотрим его свойства делимости как бинарного отношения.
1. Рефлексивность. Очевидно, что 

 . Значит, отношение делимости рефлексивно.
. Значит, отношение делимости рефлексивно.
2. Проверим, обладает ли отношение делимости каким-либо из свойств симметричности, антисимметричности или асимметричности. По следствию 2 к свойству 5, если 

 и
и 

 , то либо
, то либо 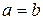 , либо
, либо  . Следовательно, ни одним из перечисленных свойств данное бинарное отношение не обладает.
. Следовательно, ни одним из перечисленных свойств данное бинарное отношение не обладает.
Заметим, что если рассмотреть отношение делимости на множестве натуральных чисел N, то окажется, что это отношение обладает свойством антисимметричности. Действительно, в этом случае следствие 2 к свойству 5 примет вид: если 

 и
и 

 , то
, то 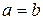 (поскольку на множестве N равенство
(поскольку на множестве N равенство  невыполнимо).
невыполнимо).
3. Транзитивность отношения делимости означает, что если 

 и
и 

 , то
, то 

 . Докажем, что отношение делимости транзитивно. Действительно,
. Докажем, что отношение делимости транзитивно. Действительно,



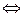
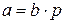 , где
, где 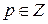 ;
;



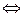
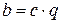 , где
, где  .
.
Следовательно, 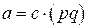 , при этом, очевидно,
, при этом, очевидно,  , а это и означает, что
, а это и означает, что 

 .
.
Таким образом, на множестве натуральных чисел N отношение делимости является отношением нестрогого порядка.
Деление с остатком
Определение 2.1. Пусть  и
и  – целые числа. Разделить число
– целые числа. Разделить число  на число
на число  с остатком, значит найти такие целые числа
с остатком, значит найти такие целые числа 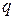 и
и 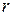 , что выполняются условия:
, что выполняются условия:
1) 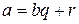
2) 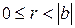 .
.
При этом 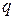 называется неполным частным, а
называется неполным частным, а 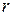 – остатком от деления
– остатком от деления  на
на  .
.
Примеры. 1) Разделить 5 на 3 с остатком. В соответствии с определением представим число 5 в виде: 5=3 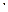 1+2. Здесь
1+2. Здесь 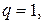
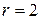 . Условие 2 из определения, очевидно, выполняется.
. Условие 2 из определения, очевидно, выполняется.
2) Разделить (–5) на 3 с остатком: (–5)=3 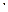 (–2)+1. Здесь
(–2)+1. Здесь 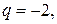
 ;
; 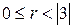 .
.
3) Разделить 5 на (–3) с остатком: 5=(–3) 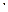 (–1)+2. Здесь
(–1)+2. Здесь 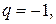
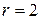 ;
;  .
.
4) Разделить (–5) на (–3) с остатком: (–5)=(–3) 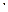 2+1. Здесь
2+1. Здесь 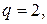
 ;
;  .
.
Теорема 2.1. Пусть  и
и  – целые числа, причем
– целые числа, причем  . Число
. Число  всегда можно разделить на число
всегда можно разделить на число  с остатком, причем единственным образом.
с остатком, причем единственным образом.
Доказательство. Рассмотрим случай, когда 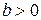 ,
,
1) Пусть 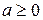 . Рассмотрим последовательность чисел:
. Рассмотрим последовательность чисел: 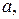
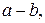
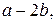 … Поскольку
… Поскольку 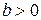 , начиная с некоторого члена этой последовательности, все члены будут отрицательными. Пусть последним из неотрицательных членов будет число
, начиная с некоторого члена этой последовательности, все члены будут отрицательными. Пусть последним из неотрицательных членов будет число 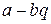 . Положим
. Положим 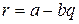 . Тогда
. Тогда 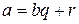 , где
, где 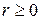 . Докажем, что
. Докажем, что  . Запишем это неравенство в виде
. Запишем это неравенство в виде 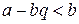 . Если бы это неравенство не выполнялось, то
. Если бы это неравенство не выполнялось, то 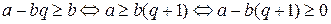 . Последние неравенство противоречит тому, что
. Последние неравенство противоречит тому, что 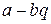 является последним неотрицательным числом в последовательности. Таким образом мы доказали, что число
является последним неотрицательным числом в последовательности. Таким образом мы доказали, что число  делится на
делится на  с остатком.
с остатком.
2) Пусть 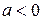 . Рассмотрим последовательность чисел:
. Рассмотрим последовательность чисел: 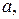

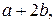 … Поскольку
… Поскольку 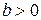 , начиная с некоторого члена этой последовательности, все члены будут положительными. Пусть
, начиная с некоторого члена этой последовательности, все члены будут положительными. Пусть 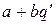 – первое неотрицательное число в этой последовательности. Положим
– первое неотрицательное число в этой последовательности. Положим 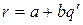 . Тогда
. Тогда 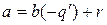 , где
, где 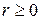 . Докажем, что
. Докажем, что  . Запишем это неравенство в виде
. Запишем это неравенство в виде 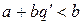 . Предположим, что неравенство не выполняется, тогда
. Предположим, что неравенство не выполняется, тогда 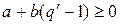 . Но
. Но 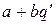 – первое неотрицательное число в последовательности. Полученное противоречие доказывает, что сделанное нами предположение неверно. Положим
– первое неотрицательное число в последовательности. Полученное противоречие доказывает, что сделанное нами предположение неверно. Положим 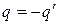 , тогда
, тогда 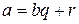 .
.
Таким образом, мы доказали возможность деления с остатком для любых целых чисел  и целых положительных чисел
и целых положительных чисел  .
.
Случай, когда 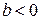 , рассматривается аналогично.
, рассматривается аналогично.
3) Докажем, что при делении одного целого числа на другое неполное частное и остаток определяются единственным образом. Пусть 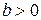 .
.
Предположим, что 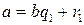 и
и 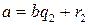 , где
, где 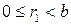 и
и  . Тогда
. Тогда 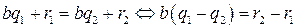 . Поскольку
. Поскольку 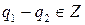 , из последнего равенства следует, что
, из последнего равенства следует, что 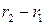

 . По свойству 5 делимости чисел, если
. По свойству 5 делимости чисел, если 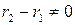 , то
, то 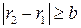 , что невозможно в силу условий
, что невозможно в силу условий 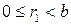 и
и  . Следовательно,
. Следовательно, 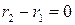 , а, значит, и
, а, значит, и 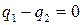 . Случай, когда
. Случай, когда 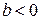 , рассматривается аналогично.
, рассматривается аналогично.
Дата добавления: 2021-02-19; просмотров: 542;











