Информационный диагностический тест, близкий к минимальному (метод Синдееева)
Этот метод реализует безусловный алгоритм диагностики. Основой этого алгоритма является ТФН, у которой столбцы соответствуют всем возможным состояниям, а строки – всем возможным проверкам (проверка πi означает контроль выхода zi). Предполагаем, что все n состояний системы, состоящей из n блоков, равновероятны и сумма вероятностей состояний их отказа равна 1, т.е. проверки, как случайные события, образуют полную группу событий:
P1=P2=…=Pn= 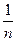 . (8)
. (8)
Тогда с точки зрения теории информации неопределённость (энтропия) Н, создаваемая такой схемой для пользователя, в общем случае определяется с помощью формулы Шеннона:
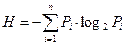 ,
,
где Pi – вероятность i – го события (вероятность отказа i – го блока
системы).
Для рассматриваемого случая из (8) получим формулу Хартли:
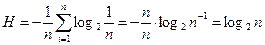 , (9)
, (9)
Для определения состояния схемы необходимо провести эксперимент, состоящий в последовательном выборе не более m наиболее информативных проверок (m<n).
Каждая k – ая проверка πk несет некоторое количество информации I относительно начального состояния (начальной энтропии Н0) рассматриваемой схемы (системы).
I=H0-H(πk)=∆H, (10)
где H(πk) – средняя условная энтропия состояния схемы после проведения проверки πk, k= 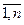 .
.
Т.к. при проведении проверки πk имеется только два возможных исхода (положительный πk и отрицательный 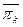 ), т.е. πk=1 или
), т.е. πk=1 или 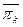 =0 с вероятностями соответственно Р(πk) и P(
=0 с вероятностями соответственно Р(πk) и P( 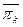 ), то средняя условная энтропия Н(πk) равна
), то средняя условная энтропия Н(πk) равна
H(πk)= Р(πk)H(πk)+P( 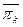 )H(
)H( 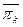 ), (11)
), (11)
где Н( 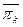 ) и Н(πk) – энтропия состояний схемы после выполнения проверки πk соответственно для отрицательного и положительного её исходов.
) и Н(πk) – энтропия состояний схемы после выполнения проверки πk соответственно для отрицательного и положительного её исходов.
Р(πk)= 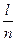 , (12)
, (12)
Р( 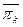 )=
)= 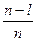 , k=1…n, (13)
, k=1…n, (13)
где 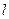 - число единиц в рассматриваемой kой строке ТФН.
- число единиц в рассматриваемой kой строке ТФН.
Тогда подставляя формулы (12) и (13) в формулу (11), а затем (11) в (10) получим с учетом (9):
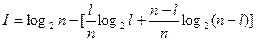 . (14)
. (14)
Информация по формуле (14) вычисляется для каждой строки ТФН. Первой для теста выбирается проверка πk, которая приносит максимум информации. Если таких проверок несколько, то выбирается любая из них, что возможно, когда информация вычисляется для равновероятных событий (отказов блоков системы) по формуле Хартли.
Если вероятности состояний P(Sj) блоков устройства не одинаковы, то энтропия (неопределенность) в оценке состояния объекта диагностики (ОД) вычисляется по формуле Шеннона (1). В этом случае вероятность отказа P(Sj) j – го блока системы можно оценить по формуле
Pj= P(Sj)= 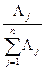 ,
,
где 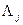 - интенсивность отказов j – го блока, час-1;
- интенсивность отказов j – го блока, час-1;
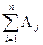 - интенсивность отказов системы, равное сумме интенсивностей отказов составляющих её блоков.
- интенсивность отказов системы, равное сумме интенсивностей отказов составляющих её блоков.
Строка ТФН, соответствующая лучшей по условию (3) проверке, перемещается на место первой строки ТФН и делит последнюю на две, в общем случае, неравные части, в одну из которых входят столбцы состояний Sj, которым соответствуют “0” в выбранной (лучшей на первом шаге) строке, а в другую – столбцы состояний, которым соответствуют “1” в выбранной строке. Выбранная на первом шаге лучшая по информативности строка больше не участвует в отборах на втором и последующих шагах формирования тестовых проверок.
Успешной (положительной) считается проверка, при которой выход контролируемого блока системы соответствует техническим условиям (ТУ) предприятия-изготовителя. Результаты успешной проверки обозначаются как диагностическая 1. В противном случае проверка считается неуспешной (отрицательной) и обозначается как диагностический 0 в ТФН и других документах.
Выбор второй наиболее информативной проверки проводится одновременно по двум полученным подТФН.
Второй выбирается проверка πi, которая обладает наибольшей условной информацией I(πk/πi) относительно состояния, характеризуемого энтропией H(πk) после первой выбранной проверки.
I(πk/πi)=H(πk) - H(πk/πi) → max (15)
Средняя условная энтропия схемы после 2ой проверки.
Н(πi/πk)= Р(πi/πk)H(πi/πk)+P( 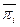 /πk)H(
/πk)H( 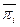 /πk)+
/πk)+
+Р(πk/ 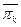 )Н ( πi/
)Н ( πi/ 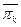 )+P(
)+P( 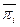 /
/ 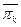 )H(
)H( 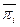 /
/ 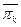 ), (16)
), (16)
где Р(πi/πk)= 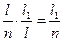 - вероятность второй успешной проверки после
- вероятность второй успешной проверки после
успешной первой. (17)
P( 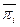 /πk)=
/πk)= 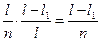 - вероятность второй неуспешной проверки
- вероятность второй неуспешной проверки
после успешной первой. (18)
P(πi/ 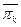 )=
)= 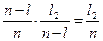 - вероятность успешной второй после неуспешной первой проверки. (19)
- вероятность успешной второй после неуспешной первой проверки. (19)
P( 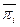 /
/ 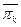 )=
)= 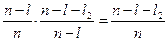 - вероятность неуспешной второй проверки после неуспешной первой. (20)
- вероятность неуспешной второй проверки после неуспешной первой. (20)
l1 и l2 – число единиц в i-ой строке подТФН №2.1 и подТФН №2.2 соответственно, первая из которых соответствует l-единицам, а вторая – (n-l) – нулям в kой – строке исходной ТФН. Из формулы (9) следует
H(πi/πk)= 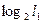 , H(
, H( 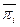 /πk)=
/πk)= 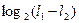 , H(πk/
, H(πk/ 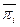 )=
)= 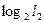 ,
,
H( 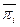 /
/ 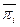 )=
)= 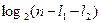 .
.
Тогда средняя условная энтропия после 2го шага
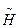 (πi/πk)=
(πi/πk)= 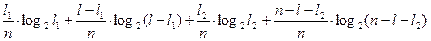 . (21)
. (21)
Информация после 2го шага для i-той строки будет равна разности выражения в квадратных скобках в уравнении (14) и выражения (21).
Вторая лучшая проверка πi из группы наиболее информативных проверок, записывается второй в исходной ТФН и не участвует в отборе на третьем и последних шагах и т.д.
Выбор проверок продолжается до тех пор, пока средняя угловая энтропия после проверки на каком-то шаге не станет равной нулю. Эта проверка и будет последней в последовательности наиболее информативных, вошедших в тест.
Если отбор проверок для теста заканчивается на m-ом шаге (m<n), то m строк, переставленные вверх по указанным выше правилам в исходной ТФН, автоматически формируют таблицу кодов неисправностей. Причем m – разрядный двоичный код каждой одиночной неисправности читается сверху вниз в каждом столбце ТФН с переставленными вверх наиболее информативными строками (проверками), образующими тестовый набор проверок.
На практике выполняются проверки состояний выходов блоков, вошедших в тестовый набор, в той последовательности, в какой они указаны в тесте. Результат каждой проверки фиксируется в виде диагностической 1 или 0. Комбинация результатов проверок, образующая двоичный код, сравнивается с таблицей кодов неисправностей, которая, как указано выше, автоматически получается из исходной ТФН и состоит из m наиболее информативных строк.
Пример реализации комбинационного метода поиска диагностики неисправностей, реализующего безусловный алгоритм диагностики по методу Синдеева.
Найти информационный тест и таблицу кодов неисправностей для схемы рис.1, в которой имеет место одиночный отказ.
1. Диагностические оценки входных и выходных сигналов:
Z5=0 – const, x1=1 – const, x2=1 – const.
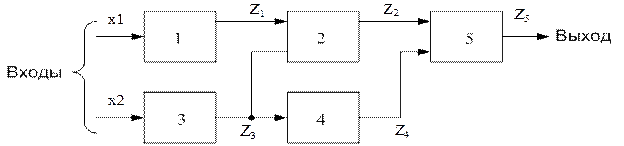
Рис.15
2. Найдем информацию, которую может принести каждая проверка на
первом шаге. В этом случае
I(πk)=H0 - log2n,
где H0 – исходная энтропия.
H0=log25=lg5/lg2=3.332 lg5=2.329бит.
ТФН, соответствующая ФДМ на рис.15 представлена табл. 2.
Таблица 2
ТФН для информационного теста
| Si πi | S1 | S2 | S3 | S4 | S5 | I(πk), бит | I(πi/πk) |
| П1 П2 | 0.729 0.975 | 0.554 - | |||||
| П3 П4 | 0.729 0.975 | 0.55 0.954 |

ТФН 2.1 ТФН 2.2
Определим среднюю условную энтропию Н(π2) схемы, которую получим в результате проведения проверки π2. Согласно (4) и (7)
H(πk)= 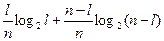 .
.
Для второй проверки
Н(π2)= 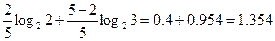 бит
бит
Тогда информация I(π2), полученная в результате проведения проверки π2, составит:
I(π2)=H0-H(π2)
I(π2)=2.329-1.354=0.975 бит.
I(π1)= 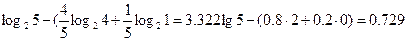 бит,
бит,
I(π3)= 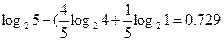 бит,
бит,
I(π4)= 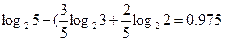 бит.
бит.
Столбец с вычисленными количествами информации поместим 6-ым в таблицу 1 функций неисправностей (ТФН), соответствующую функционально-диагностической модели (ФДМ) устройства на рис.1. На пересечении j-го столбца и i-й строки πi в таблице 1 ставится “1”, если при возникновении одиночной неисправности в j-ом блоке устройства сигнал на выходе i-го блока остается соответствующим техническим условиям (ТУ) его эксплуатации и ставится “0” в противном случае.
Первой в тест выбираем проверку π2 (контроль выхода блока 2), т.к. она приносит максимум информации и “удачно” делит исходную ТФН на две неравные части ТФН 2.1 и ТФН 2.2, первой из которых соответствуют нули в выбранной строке π2, а второй - “1”.
3. На втором шаге определим среднюю условную энтропию после второй проверки, которая включает оставшиеся проверки π1, π3, π4. Например,
H(π1/π2)= 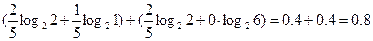 бит.
бит.
Тогда I(π1/π2)= 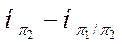 =1.354-0.8=0.554 бит.
=1.354-0.8=0.554 бит.
Аналогично H(π3/π2) 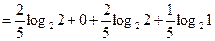 =0.4+0.4=0.8 бит.
=0.4+0.4=0.8 бит.
I(π3/π2)=1.354-0.8=0.554 бит.
Затем H(π4/π2)= 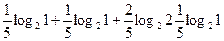 =0.4 бит,
=0.4 бит,
Следовательно I(π4/π2)=1.354-0.4=0.954 бит.
Вычисленные количественные оценки информации на втором шаге I(πi/πk) поместим в 7-ом столбце табл. 2.
Анализируя содержимое этого столбца, на втором шаге выбираем 4ую проверку π4 т.к. она несет наибольшее количество информации относительно энтропии, оставшейся после 1ой, выбранной нами проверки π2.
4. Перед выбором третьей информативной проверки перенесем на вторую строку исходной ТФН содержимое строки π4, соответствующей выбранной проверке. Указанная ситуация отображена в табл. 3, где место первой строки занимает информация строки (проверки) π2, выбранной на первом шаге. Тогда остаются две альтернативные проверки π1 и π3. Содержимое строк π1 и π3 распределяется в таблице 2 по четырем подТФН, причем ТФН 3.1 и ТФН 3.2 строятся на базе ТФН 2.1, а ТФН 3.3 и ТФН 3.4 - на базе ТФН 2.2.
Таблица 3.
ТФН для выбора 3-ей проверки теста
| Si πi | S1 | S2 | S3 | S4 | S5 | I(πf/π4/π2) |
| П2 П4 | - - | |||||
| П1 П3 | 0.4 |
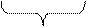
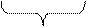
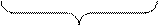

ТФН 3.1 ТФН 3.2 ТФН 3.3 ТФН 3.4
 |
ТФН 2.1 ТФН 2.2
ТФН 3.2, 3.3 и 3.4 вырождаются в столбцы, что облегчает выбор проверок и указывает на быстрое завершение формирования теста.
Информация, доставляемая третьей проверкой I(πn/πm/πk) определяется по формуле:
I(πn/πm/πk)=H(πm/πk)-H(πn/πm/πk).
Например, если третьей будет проверка π1, то
H(π1/π4/π2)= 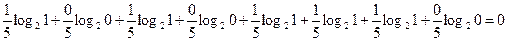
т.е. I(π3/π4/π2)= 0.4-0 = 0.4 бит.
Если третьей будет π3, то
H(π3/π4/π2)=
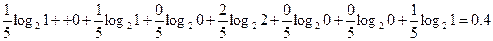 бит.
бит.
Следовательно, I(π3/π4/π2)=0.4-0.4=0 бит, т.е. проверки надо прекратить!
Располагая проверки π2,π4,π1 последовательно друг за другом, получим таблицу кодов неисправностей с трёхразрядными двоичными кодами одиночных неисправностей, которые могут иметь место в устройстве на рис.15. Такое расположение проверок сформировано в табл. 2. Код неисправности 1-го блока (состояние устройства S1) составляет 010, код состояния S2 – 011, код состояния S3 – 001, код состояния S4 – 101 и код состояния S5 –111.
Выполняя на практике последовательно проверки π2,π4,π1 (проверяя выходы Z2,Z4,Z1) и фиксируя результаты проверок в виде диагностических “0” или “1”, получают трёхразрядную двоичную комбинацию и идентифицируют неисправность в устройстве, сравнивая полученную комбинацию с таблицей кодов неисправностей.
Дата добавления: 2016-06-22; просмотров: 2676;











