Тестовый контроль дискретных комбинационных схем
Тестовый контроль предназначен для определения характера и места нахождения неисправности. При этом имеются в виду неисправности типа разрыв цепи и короткое замыкание.
Рассмотрим принцип тестового контроля применительно к комбинационным схемам. Будем считать, что в рассматриваемой схеме одновременно может быть только одна неисправность – разрыв, эквивалентный постоянному логическому нулю, или короткое замыкание, эквивалентное постоянной логической единице .
Пусть мы имеем логическую схему S0 в исправном состоянии. Она реализует логическую функцию 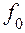 (x1,x2, … ,xn), называемую функцией исправной схемы.
(x1,x2, … ,xn), называемую функцией исправной схемы.
При наличии i-й неисправности схема S0 переходит в схему Si, реализующую новую функцию 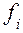 (x1,x2, … ,xn), называемую функцией неисправности.
(x1,x2, … ,xn), называемую функцией неисправности.
Рассмотрим комбинационную схему, представленную на рисунке 1, и для неё запишем все функции неисправности.
Функция исправной схемы выглядит следующим образом :


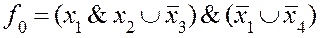
Для неисправностей типа “короткое замыкание” функции неисправностей имеют вид:
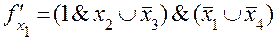 при
при 
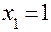 ;
;
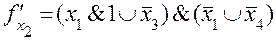 при
при 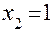 ;
;
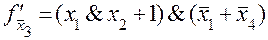 при
при 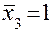 ;
;
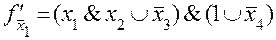 при
при 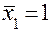 ;
;
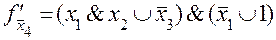 при
при 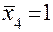 .
.
Для неисправности типа “разрыв” функции неисправностей имеют вид:
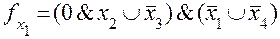 при
при 
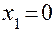 ;
;
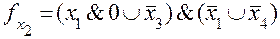 при
при 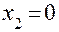 ;
;
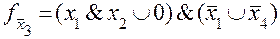 при
при 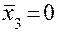 ;
;
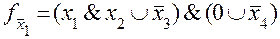 при
при 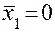 ;
;
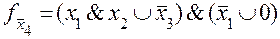 при
при 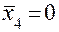 .
.
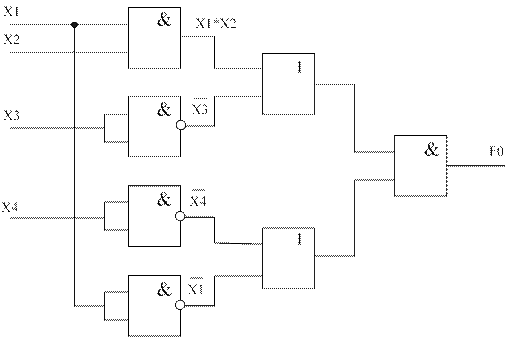
Рис.13. Комбинационная схема №1
По выражениям исправной и неисправной схем строится таблица функций неисправностей, в которую записывают все наборы значений аргументов и значения функций исправной схемы, вычисленные на этих наборах. Для рассматриваемого случая наборы функций неисправностей представлены в таблице 1. В верхней части таблице выделены наборы, на которых 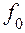 =1 и записаны функции неисправностей при разрывах, отличающиеся от значений функции
=1 и записаны функции неисправностей при разрывах, отличающиеся от значений функции 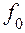 . В нижней части таблицы выделены наборы, на которых
. В нижней части таблицы выделены наборы, на которых 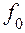 =0, и записаны значения функций неисправностей при “коротком замыкании”, отличающийся от функции
=0, и записаны значения функций неисправностей при “коротком замыкании”, отличающийся от функции 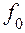 .
.
По таблице функций неисправностей можно осуществить поиск неисправностей. Пусть при реализации всех значений наборов аргументов из верхней части таблицы на выходе схемы получен, например, сигнал логического“0” только на наборах e1 и e5. Из таблицы видно, что реализуется схемой в этом случае только функция 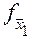 . А это значит, что имеет место разрыв контакта
. А это значит, что имеет место разрыв контакта 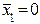 .
.
Такой способ поиска неисправностей предполагает реализацию всех наборов значений аргументов.
Таблица 1
| Наборы значений аргументов | 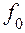
| Значение функции неисправностей при «к.з.» | Значение функции неисправностей при «разрыве.» | ||||||||||||
| X1 | X2 | X3 | X4 | 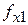
| 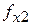
| 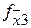
| 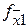
| 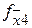
| 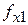
| 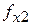
| 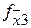
| 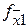
| 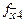
| ||
| e0 | |||||||||||||||
| e1 | |||||||||||||||
| e4 | |||||||||||||||
| e5 | |||||||||||||||
| e8 | |||||||||||||||
| e12 | |||||||||||||||
| e14 | |||||||||||||||
| e2 | |||||||||||||||
| e3 | |||||||||||||||
| e6 | |||||||||||||||
| e7 | |||||||||||||||
| e9 | |||||||||||||||
| e10 | |||||||||||||||
| e11 | |||||||||||||||
| e13 | |||||||||||||||
| e15 |
Рассмотрим методику отыскания неисправностей путём использования лишь некоторого количества наборов, а не всех полностью.
Пусть мы имеем М-множество функций неисправностей, включающее и функцию исправной схемы, заданных на множестве Е наборов значений аргументов. Пусть далее все функции из множества М попарно различимы и имеется множество Р пар функций неисправностей вида: 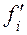 ,
, 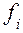 и множество Р всех возможных пар функций неисправностей за исключением пар
и множество Р всех возможных пар функций неисправностей за исключением пар 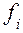 ,
, 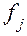 . Тогда диагностическим тестом ( относительно Е, М, Р) называется множество наборов аргументов Тg
. Тогда диагностическим тестом ( относительно Е, М, Р) называется множество наборов аргументов Тg 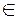 Е, на котором все функции неисправностей (
Е, на котором все функции неисправностей ( 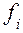 ,
, 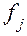 ) попарно различимы.
) попарно различимы.
Таким образом, для поиска неисправностей достаточно проверить схему не на всех наборах значений аргументов, а только на тех, которые входят в соответствующий тест. Как правило Тg <Е, вследствие чего проверка оказывается более короткой.
Как определить наборы, которые входят в тест Тg?
В общем случае функции 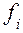 и
и 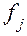 могут различаться не на одном наборе, а на некотором множестве наборов. Поэтому для каждой пары функций неисправностей можно составить функцию таких наборов.
могут различаться не на одном наборе, а на некотором множестве наборов. Поэтому для каждой пары функций неисправностей можно составить функцию таких наборов.
e1 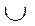 e2
e2 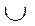 . . . ek =
. . . ek = 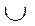 em . (4)
em . (4)
Для того, чтобы все пары функций неисправностей были одновременно различимы, необходимо образовать конъюнкцию полученных дизъюнкций.
& 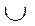 em (5)
em (5)
Затем (5) преобразуется в дизъюнкцию конъюнкций 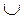 & по правилам алгебры логики в предположении, что каждый входной набор отождествляется с логической переменной.
& по правилам алгебры логики в предположении, что каждый входной набор отождествляется с логической переменной.
Каждое слагаемое (конъюнкция) полученного выражения будет представлять собой диагностический тест.
Выражение (4) для каждой пары функций неисправностей составляется по таблице функций неисправностей. С этой целью сравниваются значения функций на каждом из наборов значений аргументов и выписываются дизъюнкции наборов всех пар функций неисправностей, то есть составляются выражения (4). Затем составляется конъюнкция дизъюнкций (5), после чего полученные выражения преобразуются в дизъюнкцию конъюнкций.
Каждая конъюнкция наборов будет диагностическим тестом.
Рассмотрим алгоритм получения тестов:
В таблице функций неисправностей вычёркиваются строки, содержащие значения функций либо только с нулями, либо только с единицами;
Из группы неразличимых строк остаётся одна, остальные вычёркиваются;
Для каждой пары функций неисправностей составляется дизъюнкция наборов значений аргументов, при которых эти функции отличаются друг от друга;
Из полученных выражений (4) составляются выражения (5), для чего в начале выписываются одночленные дизъюнкции. Многочленные дизъюнкции, в которые входит набор из числа выписанных одночленных дизъюнкций, вычёркиваются на основании операций поглощения. Из остальных выражений выписываются двучленные дизъюнкции и вычёркиваются те многочлены, которые содержат любую двучленную дизъюнкцию и т.д.;
Выражение, полученное в пункте 4, преобразуется в дизъюнкцию конъюнкций.
Каждая конъюнкция при этом будет диагностическим тестом.
Построим диагностический тест для поиска неисправностей типа “разрыв”в схеме на рисунке 1.
Для построения теста используется верхняя часть таблицы 1.
Произведем поиск неисправности по алгоритму, изложенному выше:
- пункт 1 алгоритма к данному примеру неприменим, так как среди значений неисправностей при разрыве нет строк только с одними единицами;
- по пункту 2 алгоритма вычёркиваем строки e4 и e5;
- по пункту 3 составляем дизъюнкцию наборов для каждой пары функций, на которых они отличаются друг от друга.
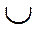
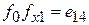 ;
;
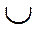
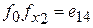 ;
;
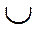
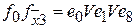 ;
;
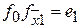 ;
;
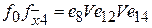 ;
;
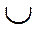
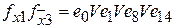 ;
;
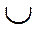
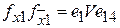 ;
;
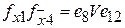 ;
;
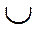
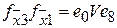 ;
;
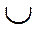
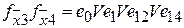 ;
;
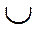
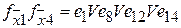 .
.
Просмотрев полученные дизъюнкции, видим, что одночленные дизъюнкции e1 и е14 поглощают все остальные за исключением е8 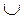 е12 и е0
е12 и е0 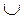 е3.
е3.
Тогда конъюнкция дизъюнкций будет иметь вид:
& 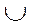 = e1 & e14 & (e8
= e1 & e14 & (e8 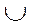 e12) & (e0
e12) & (e0 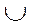 e3) . (6)
e3) . (6)
По пункту 5 преобразуем выражение (6), используя распределительный закон:
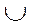 &= e0 & e1 & e8 & e14
&= e0 & e1 & e8 & e14 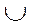 e1 & e12 & e14 & e3
e1 & e12 & e14 & e3 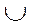 … (7)
… (7)
Таким образом, получаем равноценные тесты (конъюнкции), каждый из которых состоит из четырёх наборов:
T1= e0 & e1 & e8 & e14 , T2= e1 & e12 & e14 & e3 …
Реализация любого из них достаточна для поиска неисправностей типа “разрыв”.
Построение тестов для “к.з.” аналогично и осуществляется по нижней части таблицы 1.
Поиск неисправности осуществляется путем подачи в произвольно выбранной последовательности наборов теста и фиксации состояний входа. Для этого необходимо закодировать неисправности. Принцип кодирования неисправностей заключается в следующим. Для каждого набора теста по таблице функции неисправности записывается состояние выхода схемы, соответствующее конкретной неисправности. При этом учитывается выбранная последовательности записи наборов в тесте. В результате получаем двоичные числа (коды), каждое из которых описывает поведение схемы при конкретной неисправности.
В ходе “прогонки” теста фиксируются действительные значения выходов схемы, и после реализации всех тестовых наборов производится последовательное сравнение полученного двоичного числа с кодом каждой неисправности, по которому она и определяется.
Для поиска неисправности типа: ”разрыв в схеме ” на рис.13 возьмём тест Т1 и произведем кодирование неисправностей.
Для наглядности тест представим в виде графа, вершинами которого будут являться наборы тестов, а ребра обозначают значения выходов схемы и функции, которые реализуются при данных значениях.
Таблица функций неисправностей
| Наборы значений аргументов | 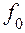
| Значение функции неисправностей при «к.з.» | Значение функции неисправностей при «разрыве.» | ||||||||||||
| X1 | X2 | X3 | X4 | 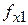
| 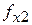
| 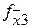
| 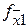
| 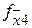
| 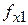
| 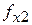
| 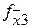
| 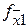
| 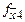
| ||
| e0 | |||||||||||||||
| e1 | |||||||||||||||
| e4 | |||||||||||||||
| e5 | |||||||||||||||
| e8 | |||||||||||||||
| e12 | |||||||||||||||
| e14 | |||||||||||||||
| e2 | |||||||||||||||
| e3 | |||||||||||||||
| e6 | |||||||||||||||
| e7 | |||||||||||||||
| e9 | |||||||||||||||
| e10 | |||||||||||||||
| e11 | |||||||||||||||
| e13 | |||||||||||||||
| e15 |
Граф тестовых проверок на обрыв (лог. 0 – const ):
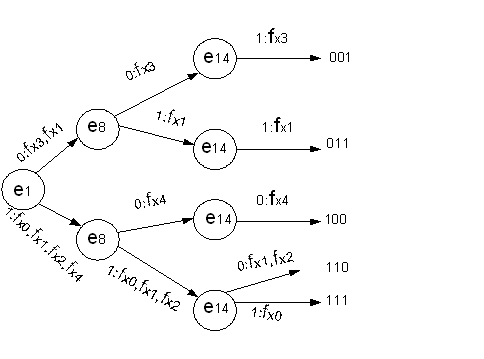
Рис.14
Дата добавления: 2016-06-22; просмотров: 2760;











