Метод критерия различимости – комбинационный метод, реализующий безусловный алгоритм диагностики

1) Постановка задачи

Проблема заключается в том, что разработать набор тестов, который будет иметь дело со всеми неисправностями цифровой системы. Однако, одни методы генерирования тестов вырабатывают их лишь для однократной специфической неисправности, не пригодны в столь больших схемах. Очевидное решение – применить некоторый метод многократно до полной обработки неисправностей. А затем полученные тесты объединить. Однако набор тестов, полученных таким способом неприемлем из-за емкости потребляемой памяти и времени обработки. Отсюда возникает задача сокращение объема набора теста.

2) Таблица неисправностей – используется для представления результатов генерирования тестов, является двух мерным массивом, имеющем по одной строке на каждую неисправность и по одному столбцу на каждый тест. Для элемента таблицы :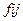

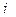=1, если -я неисправность обнаруживается 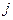-м тестом и

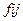=0 – в противном случае.

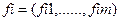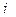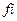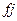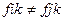
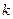Строка называется отображениями неисправности и является вектор–строками, - отображение -й неисправности. Два отображения неисправности и различимы , если для некоторого , где 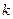- номер теста. Таким образом задача трансформируется в задачу нахождения минимального набора столбцов таблицы так, чтобы каждая строка, соответствующей подтаблицы имела бы по крайней мере одну «1». Чтобы различать все неисправности необходим минимальный набор столбцов, соответствующий вышеизложенным требованиям и имеющий все различимые строки.

3) Метод критерия различимости.

Основная идея – в приписывании весов отдельным тестам. Веса отражают относительную способность тестов различать неисправности.

На основе весов отбираются тесты для получения эффективного набора тестов.

Вес 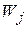теста 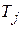определяется как и число пар неисправностей, которые он различает:

,

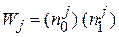где 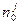и 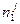- число соответственно «0» и «1» в 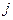-м столбце таблицы

Метод строится на последовательности итераций. Вычисляются 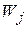для всех 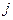. Затем в качестве первого выбирается тест с max 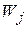, так как он различает наибольшее число пар неисправностей. Этот тест делит неисправности на обнаруживаемые и необнаруживаемые. В общем случае, когда выбран 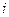-й тест, неисправности будут разделены на 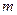непересекающихся блоков 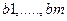. Это означает, что последующие тесты должны выбираться более сложным путем.

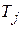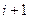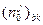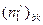Пусть кандидат на ( ) элемент набора и пусть и - число «0» и «1» в 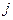-м столбце блока 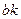. Тогда после 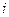-го шага вес для 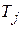будет равен:

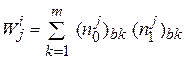
Тест, для которого 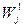-max, выбирается как 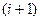элемент набора тестов. Отбор тестов продолжается до тех пор, пока разделение неисправностей перестанет приносить дальнейшее улучшение, т.е. до тех пор, пока веса всех неиспользованных «тестов» не станет равное «0» (не станет «0» или «1» )

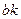Развитие метода

Возможен отбор тестов, которые диагностируют неисправности с заданной степенью диагностической разрешающей способности, которая зависит от объема схемы, содержащейся в каждой сменной ячейке.

Развитие метода – выбор набора тестов, которые идентифицируют неисправность только с точностью до одной БИС – ячейки.

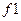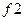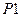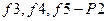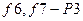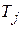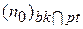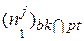Предположим: неисправности и связаны с ячейкой ; ; . Ясно, что мы не хотим больше различать пары неисправностей из одной и той же ячейки, вклад таких пар в вес теста нужно вычитать для при условии, что и - число «0» и «1» в j-м столбце блока bk, связанного с ячейкой pl. Тогда выполняется соотношение

,

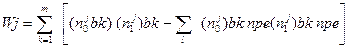где суммирование производится по всем ячейкам, связанным с блоком 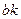( 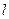- число сменных ячеек, 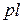– одна из ячеек, ).

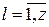Пример: Таблица неисправностей (рис.16) состоит из восьми тестов и двенадцати неисправностей. Объект реализован на пяти сменных ячейках P₁-P₅.

В ячейке P₁ необходимо обнаруживать две неисправност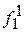и и 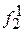, во второй P₂ и четвертой P₄ – по три неисправности, в третьей P₃ и пятой P₅ ячейках – по две неисправности.

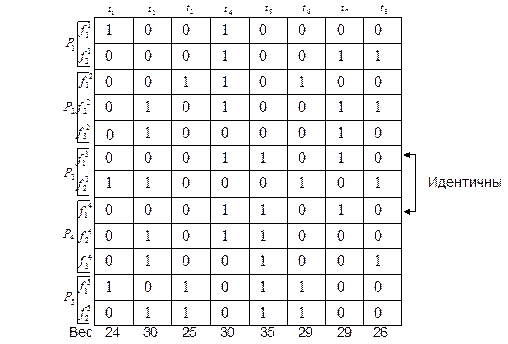
Рис 16. Таблица ТФН №1

Сначала вычисляются веса и получаем, что max весом обладает .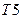

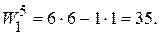
Перестраиваем таблицу 1 в таблицу 2 . Снова вычисляем веса тестов (кроме 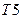). На этот раз выбор пал на .

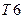Рис 17. ТНФ №2

Проиллюстрируем определение веса 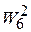для теста t₆ , лучшего на втром шаге

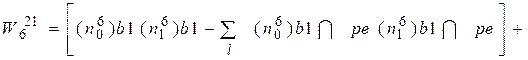
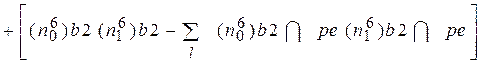
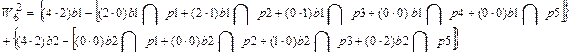
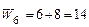
При следующей перестройке таблицы (ТФН3) блок b4 можно не рассматривать, так как его строки связаны только с Р5:

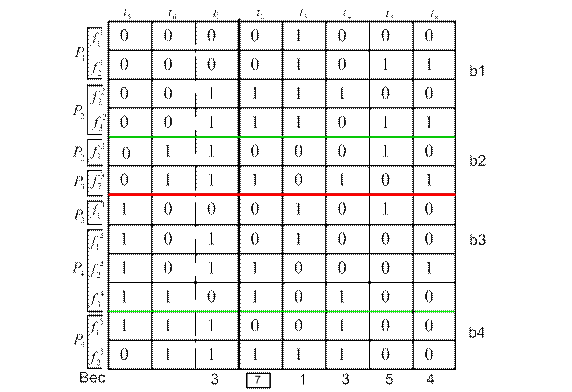
Рис 18. ТФН №3

Проиллюстрируем определение веса 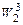столбца 2, который оказывается лучшим на третьем шаге отбора тестов.

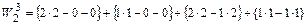
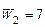
Таким образом тест Т2 выбираем третьим в группу тестов, имеющих наибольшие веса.

Следующая перестройка ТФН представлена на рис.19..

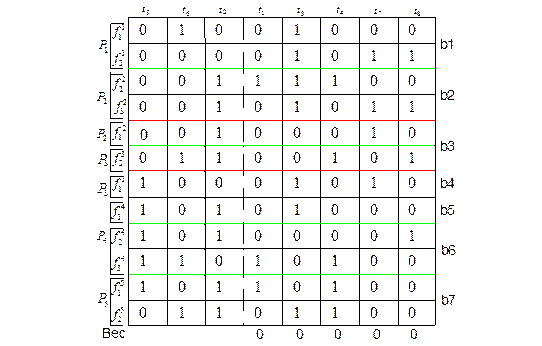
Рис 19. ТНФ №4

Теперь все тесты имеют веса = 0 – процесс отбора тестов заканчивается, минимальным набором является (Т5, Т6, Т2). Следовательно для идентификации каждой неисправной ячейки требуется только семь комбинаций:

Р1=(0,0,0) или (0,1,0); Р2=(0,0,1); Р3=(0,1,1); Р4=(1,0,1) или (1,1,1); Р5=(1,1,0)

Метод привлекателен для больших таблиц неисправностей, т.к. для реализации на машине требуется немного памяти, длина наборов тестов равна min (m,n) итераций. Неразличимые итерации автоматически группиризуются в общие группы, а процесс отбора тестов может быть изменен, чтобы учитывался любой вид ограничений, накладываемых ячейками.