Площади многоугольников

Два многоугольника называются смежными, если они имею одну или несколько общих сторон или частей сторон, но не имеют ни одной общей внутренней точки.

Если в двух данных смежных многоугольниках не рассматривать их общих сторон, то образуется третий многоугольник, который называется суммой первых двух.

Внутренняя область суммы двух многоугольников содержит внутренние точки каждого из исходных многоугольников и только эти.

Установить систему измерения площадей многоугольников, значит поставить в соответствие каждому многоугольнику положительное число, называемое его площадью, и обладающее следующими свойствами:

1. Квадрату со стороной равной единице длины соответствует число равное 1.

2. Равным многоугольникам соответствует одна и та же площадь, независимо от занимаемого ими положения в пространстве(свойство инвариантности).

3. Многоугольник, представляющий собой сумму двух многоугольников, имеет площадь, равную сумме площадей составляющих его многоугольников (свойство аддитивности).

Два многоугольника, имеющие одну и ту же площадь называются равновеликими.

Прямоугольник

Прямоугольник— четырёхугольник, у которого все углы прямые

Основанием прямоугольника называется одна из его сторон. Сторона, перпендикулярная основанию, называется высотой прямоугольника. Основание и высота прямоугольника называются его измерениями.

Теорема: Площадь прямоугольника S, стороны которого имеют длины a и b, выражается формулой S=ab.

Доказательство: Покажем, что при этом выполняются все свойства измерения площадей многоугольников.

1. Прямоугольник с измерениями 1 и 1 (т.е. квадрат со стороной 1) дает S=1×1=1.

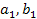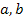2. Рассмотрим два прямоугольника с измерениями и , такие что 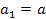, 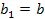. Т.е. прямоугольники равны. Площадь первого из них 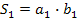, второго 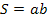, т.к. 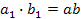, то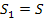

3. Рассмотрим прямоугольник с измерениями , .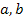

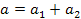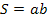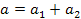Тогда , но Þ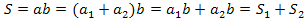

Параллелограмм

Параллелограмм– это четырёхугольник, противоположные стороны которого попарно параллельны.

Теорема: Площадь параллелограмма измеряется произведением его основания на высоту

Доказательство: самостоятельно

Треугольник

Теорема: Площадь треугольника равна половине произведения основания на высоту

Доказательство: самостоятельно

Теорема(формула Герона): Площадь треугольника может быть найдена по формуле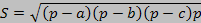

Доказательство: самостоятельно

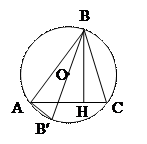Теорема: Произведение трех сторон треугольника равно учетверенному произведению площади треугольника на радиус описанной окружности: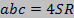

Доказательство:

Проведем высоту ВН и диаметр ВВ¢. Рассмотрим DВНС и DВАВ¢. Они оба прямоугольные (почему?

)

и Ð АВ¢В=ÐАСВ (почему?

)

Следовательно, они подобны. Значит 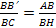откуда 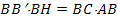. Умножая на АС обе части, получим требуемое(покажите!

)

Следствие: площадь треугольника может быть найдена как .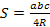

Круг

Теорема: Если в окружность вписать правильный многоугольник и описать правильный многоугольник с тем же числом сторон, которые неограниченно удваивать, то площади вписанного и описанного многоугольников будут стремиться к одному и тому же пределу, называемому площадью круга.

Доказательство: самостоятельно, аналогично теореме о периметрах вписанного и описанного многоугольников

Теорема: Площадь круга измеряется половиной длины окружности, умноженной на радиус.

Доказательство: самостоятельно, аналогично теореме о длине окружности