Решение типовых задач

Пример 1.В 450 г воды растворили 50 г . Вычислить процентное содержание кристаллогидрата и безводной соли.

Решение. Общая масса раствора составляет 500 г. Процентное содержание кристаллогидрата находим из пропорции:

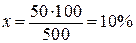
Процентное содержание безводной соли 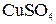составит

,

где 31,96 – количество граммов 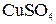, отвечающее 50 г .

Предельную растворимость вещества выражают количеством граммов вещества, которое растворяется в 100 г воды при данной температуре.

Очевидно, если предельная растворимость 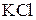при 0^°С составляет 27,6 г, то насыщенный при указанной температуре раствор содержит

.

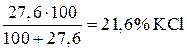Если известно, что насыщенный при 40^°С раствор 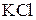содержит 28,57% растворенной соли, то предельная растворимость вычисляется из пропорции:

28,57 г соли растворены в 71,43 г воды

х » » » » 100 » »

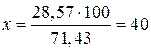г соли.

Пример 2.Сколько граммов соли и воды содержится в 800 г 12%-ного раствора ?

Решение. Масса растворенной соли составляет 12% от массы раствора, т. е.

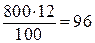г ,

а масса растворителя составляет 88% от массы раствора, т.е.

г воды.

Пример 3.Сколько граммов 3%-ного раствора 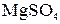можно приготовить из 100 г ?

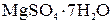Решение. В 100 г 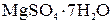содержится

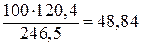г

безводной соли. Согласно условию задачи масса безводной соли составляет 3% массы раствора.

3% массы раствора составляют 48,84 г

100 » » » » х »

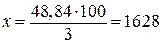г.

Пример 4.Сколько граммов 5%-ного раствора КОН можно приготовить из едкого кали и 100 г воды?

Решение. Согласно условию задачи 100 г воды составляют 95% массы всего раствора. Отсюда масса раствора равна

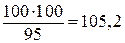г.

Пример 5.Сколько граммов 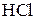следует растворить в 250 г воды для получения 10%-ного раствора ?

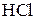Решение. 250 г воды составляют 90 % массы раствора. Масса 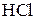составляет 10% массы раствора или

г .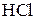

Пример 6.В каком количестве граммов воды следует растворить 100 г 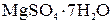для получения раствора, содержащего 5% безводной соли?

Решение. 100 г 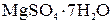содержит 48,84 г 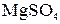и 51,16 г воды. Согласно условию 48,84 г соли составляют 5% массы раствора. Отсюда масса растворителя равна

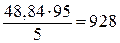г.

Следовательно, остается добавить 928 – 51,2 = 876,8 г воды.

Можно найти сначала общую массу раствора, которая составит

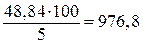г,

а затем массу растворителя:

976,8 – 100 = 876,8 г воды.

Пример 7.Сколько граммов 10%-ного раствора H₂SO₄ требуется для обменного взаимодействия с 100 мл 13,7%-ного раствора Na₂CO₃ (ρ = 1,145).

Решение. Масса 100 мл раствора составляет 114,5 г и содержит

114,5 ∙ 0,137 = 15,68 г Na₂CO₃.

Из уравнения реакции

Na₂CO₃ + H₂SO₄ = Na₂SO₄ + CO₂ + H₂O

Находим необходимое количество серной кислоты:

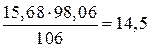г,

а 10%-ного раствора H₂SO₄ потребуется

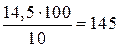г.

Пример 8.Сколько миллилитров 9,5%-ного раствора Na₂CO₃ (ρ = 1,10) следует добавить к 100 г воды для получения 3%-ного раствора?

Решение. Обозначим искомый объем раствора через x мл. Масса его в этом случае равна х · 1,10 г, а масса содержащегося в нем Na₂CO₃ равна х ∙ 1,10 · 0,095 г. Согласно уравнению задачи, масса растворенного вещества составляет 3% от массы полученного раствора (1,10х + 100):

,

х ≈ 42 мл.

Пример 9.Сколько мл 35%-ного раствора аммиака (ρ = 0,94) требуется для образования 33г (NH₄)₂SO₄?

Решение. Из уравнения реакции

2NH₃ + H₂SO₄ = (NH₄)₂SO₄

находим массу аммиака:

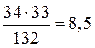г,

а 35%-ного раствора потребуется

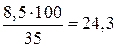г, или 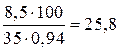мл.

Пример 10.Сколько мл 32,5%-ного раствора NH₃ (ρ = 0,888) требуется для образования сульфата аммония (NH₄)₂SO₄ с 250 мл 27,3%-ного раствора H₂SO₄ (ρ = 1,2)?

Решение. Масса раствора кислоты составляет 250 ∙ 1,2 = 300 г. Раствор содержит 300 · 0,273 = 81,9 г H₂SO₄ . Согласно уравнению

2NH₃ + H₂SO₄ = (NH₄)₂SO₄

вычисляем массу аммиака, вошедшего в реакцию; она составляет

г NH₃.

Этому количеству граммов NH₃ соответствует

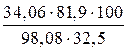г

или

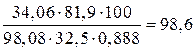мл

его 32,5%-ного раствора.

Пример 11. Вычислить молярную концентрацию, молярную концентрацию эквивалента, титр и моляльность 10% - го раствора Al₂(SO₄)₃ (ρ = 1,105 г/см³).

Решение. 1. Масса 1 л раствора т_р-ра = ρV_р-ра = 1,105 ∙1000 =115 г. По определению массовой доли, в 100 г раствора содержится 10 г Al₂(SO₄)₃, следовательно, в 1105 г (т. е. в 1 л) соответственно (1105 ·10)/100 = 110,5 г. Молярная масса Al₂(SO₄)₃ М(Al₂(SO₄)₃) = 342 г/моль. Таким образом, в 1 л раствора содержится 110,5/342 = 0,32 моль Al₂(SO₄)₃ и молярная концентрация раствора с_м равна 0,32 моль/л.

2. Эквивалент молекулы Al₂(SO₄)₃ равен 1/6 молекулы: Э(Al₂(SO₄)₃) = 1/6 (М(Al₂(SO₄)₃)). Следовательно, в одном моле Al₂(SO₄)₃ содержится шесть моль-эквивалентов, а в 1 л данного раствора 0,32 · 6 = 1,92 моль-экв Al₂(SO₄)₃. Молярная концентрация эквивалента (или нормальная концентрация) с_н равна 1,92 моль/л или 1,92 н.

3. Поскольку выше было найдено, что в 1000 мл раствора содержится 110,5 г растворенного вещества, то в 1 мл находится 110,5/1000 = 0,1105 г Al₂(SO₄)₃ и титр раствора Т = 0,1105 г/мл.

4. По условию в 100 г раствора содержится 10 г Al₂(SO₄)₃ и 90 г Н₂О. Тогда на 1000 г воды приходится (1000 · 10)/90 = 111,11 г Al₂(SO₄)₃. Это составляет 111,11/342 = 0,325 моль. Следовательно, в 1000 г растворителя содержится 0,325 моль растворенного вещества Al₂(SO₄)₃ и моляльность раствора с_т,по определению, равна 0,325 моль/1000 г Н₂О.

Пример 12.Константа диссоциации муравьиной кислоты НСООН, диссоциирующей по уравнению

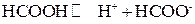
составляет 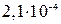. Вычислить a и для 0,3 М раствора этой кислоты.

Решение.

что соответствует 2,64 %

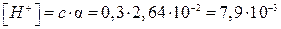моль/л;

Вариант решения. Напишем выражение для константы диссоциации в общем виде:

.

Числитель представляет собой произведение концентраций ионов; эти концентрации равны друг другу, поэтому числитель можно заменить выражением 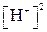. Знаменатель представляет собой концентрацию недиссоциированной части кислоты, которую, если пренебречь диссоциированной частью, примем равной общей концентрации электролита (то же допущение делается и при выводе формулы 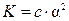, когда величина 1 - a принимается равной 1). В этом случае

Находим :

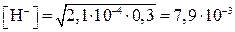моль/л;

Пример 13. Концентрация гидроксильных ионов 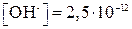моль/л. Вычислить рН.

Решение.

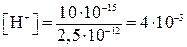моль/л,

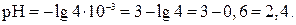
Или, если 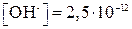моль/л, то 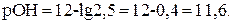Учитывая, что рН + рОН = 14, находим рН = 14 – 11,6 = 2,4.

Пример 14. рН раствора составляет 4,3. Вычислить и .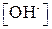

Решение.

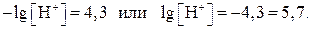
0,7 – это логарифм коэффициента, стоящего при 10^-5. Этому логарифму соответствует число 5, следовательно,

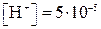моль/л, а 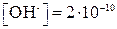моль/л.

Соотношение между рН и рОН

	Усиление кислотного характера среды	Нейтральная среда
рН
		10-1	10-2	10-3	10-4	10-5	10-6	10-7
	10-14	10-13	10-12	10-11	10-10	10-9	10-8	10-7
рОН
	Нейтральная среда	Усиление щелочного характера среды
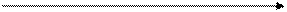
рН
	10-7	10-8	10-9	10-10	10-11	10-12	10-13	10-14
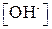
	10-7	10-6	10-5	10-4	10-3	10-2	10-1
рОН

Для вычисления рН растворов кислот и оснований следует предварительно вычислить 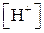или .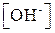

Пример 15.Вычислить рН 1/400 М раствора КОН.

Решение. Принимая, что активность иона ОН^- практически равна его концентрации, находим

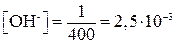моль/л;

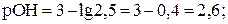
рН = 14 – 2,6 = 11,4.

Пример 16.Вычислить рН 1%-ного раствора муравьиной кислоты, считая, что плотность раствора равна 1;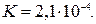

Решение. 1 л раствора содержит 10 г НСООН, что составляет 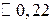моль/л.

Пример 17. Определите температуру кипения раствора, содержащего 1,84г нитробензола C₆N₅NO₂ в 10 г бензола. Эбуллиоскопическая постоянная бензола 2,53. Температура кипения чистого бензола 80,2⁰С.

Решение.

По закону Рауля

, (17)

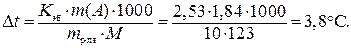
Температура кипения раствора: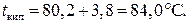

Пример 18. Раствор, содержащий 1,22 г бензойной кислоты C₆H₅COOH в 100 г сероуглерода, кипит при 46,529 ⁰С, температура кипения сероуглерода 46,3 ⁰С. Вычислите эбуллиоскопическую константу сероуглерода.

Решение.

Повышение температуры кипения ∆t = 46,529 – 46,3 = 0,229⁰. Молярная масса бензойной кислоты 122 г/моль. Из формулы (1) находим эбуллиоскопическую константу:

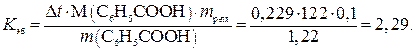
Пример 19. Раствор, содержащий 11,04 г глицерина в 800 г воды, кристаллизуется при –0,279⁰C. Вычислить молярную массу глицерина.

Решение.

Температура кристаллизации чистой воды 0⁰С, следовательно, понижение температуры кристаллизации ∆t = 0 – (– 0,279) = 0,279⁰. Подставляя в уравнение (1) данные вычисляем молярную массу глицерина: