Условие равновесия в гетерогенной системе
Рассмотрим систему, состоящую из k независимых компонентов и m фаз, находящуюся в состоянии термодинамического равновесия при р, Т = const. Общее условие равновесия в системе имеет вид:
dG = 0.
Общая энергия Гиббса складывается из энергий Гиббса каждой из фаз:
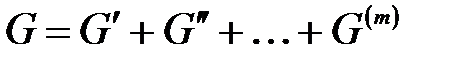 .
.
Продифференцируем:
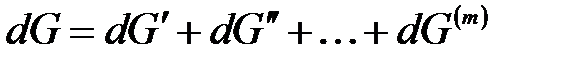 .
.
Для каждой из фаз
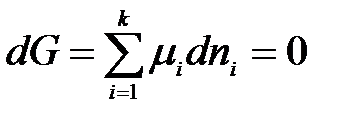 .
.
Подставим значение dG для каждой фазы:
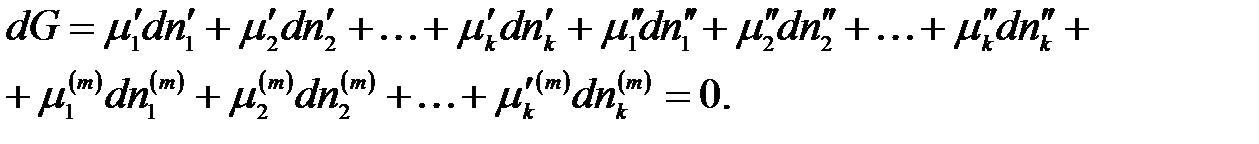
Пусть без нарушения равновесия из первой фазы во вторую перешло бесконечно малое число моль 1-го компонента. При этом числа моль всех остальных компонентов постоянны во всех фазах и значения внешних параметров не изменяются: р, Т = const. Тогда условие равновесия приобретает вид:
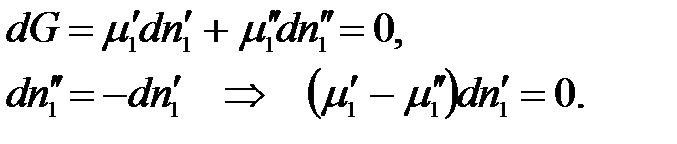
Произведение равно нулю, если хотя бы один из множителей равен нулю, но согласно условию 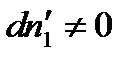 , тогда
, тогда
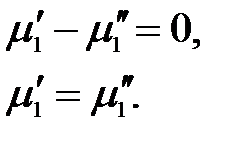
Следовательно, химический потенциал первого компонента одинаков в обеих фазах. Рассматривая аналогичные частные случаи для других компонентов и фаз, получим:
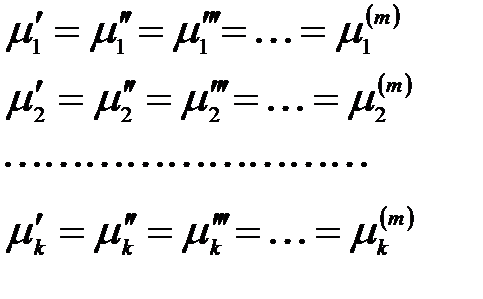
Полученное уравнение является условием равновесия в m-фазной
k-компонентной системе и называется теоремой равновесия Гиббса:
условием термодинамического равновесия в гетерогенной системе является равенство химических потенциалов каждого компонента во всех фазах при Р, Т = const или V, Т = const
В качестве примера рассмотрим двухфазную трехкомпонентную систему. Условие равновесия для такой системы имеет вид:
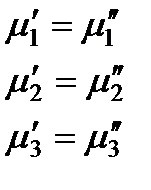 ,
,
где 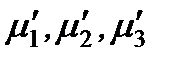 – химические потенциалы 1, 2 и 3-го компонентов в одной фазе;
– химические потенциалы 1, 2 и 3-го компонентов в одной фазе;
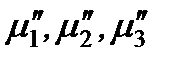 – химические потенциалы 1, 2 и 3-го компонентов в другой фазе.
– химические потенциалы 1, 2 и 3-го компонентов в другой фазе.
Правило фаз Гиббса
Пусть при р, Т = const в состоянии равновесия существует система, состоящая из k компонентов и m фаз. На систему оказывают влияние s внешних параметров (на практике обычно s = 2 – это р и Т). Поставим задачу рассчитать число термодинамических степеней свободы данной системы.
Число термодинамических степеней свободы – это число независимых параметров состояния данной системы, оно равно общему числу параметров состояния системы за вычетом числа уравнений, связывающих эти параметры.
Для определения состава любой фазы, содержащей k компонентов достаточно указать содержание (k – 1) компонентов. Так как концентрации компонентов обычно выражены в массовых или мольных долях и концентрация одного из компонентов будет определена, если известны концентрации остальных компонентов.
Например, двухкомпонентная система представляет собой 20 %-й водный раствор уксусной кислоты. Тогда массовую долю второго компонента – воды можно рассчитать: 100 – 20 = 80 %. Поэтому указывать, сколько в системе содержится воды необязательно.
Если в системе m фаз, то для описания их состава требуется m(k–1) переменных. Кроме того, на систему влияют внешние параметры, количество которых равно s. Следовательно, общее количество переменных ,влияющих на состояние системы равно:
m(k – 1) + s.
Однако не все эти переменные независимы друг от друга, та как при равновесии распределение каждого из компонентов между различными фазами должно удовлетворять теореме равновесия Гиббса:
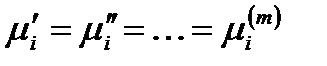
Очевидно, что таких уравнений для каждого из компонентов будет на единицу меньше числа фаз. Например, если m = 3, то для первого компонента запишется только два уравнения:
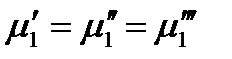 ,
,
тогда число уравнений, связывающих химические потенциалы одного компонента равно m – 1, а всех k компонентов – k(m – 1).
Для определения числа термодинамических степеней свободы вычтем из общего числа параметров, описывающих состояние данной системы число уравнений, связывающих их:
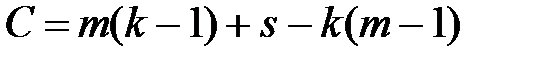
После преобразований получим:
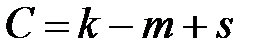 . (2.5)
. (2.5)
Уравнение (2.5) выражает основной закон фазового равновесия – правило фаз Гиббса. Если на систему влияют два внешних параметра (р и Т), то правило фаз Гиббса записывается
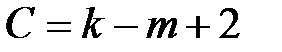 .
.
Дата добавления: 2016-06-22; просмотров: 2397;











