Некоторые свойства.
1. Линейность 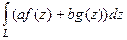 =
=  .
.
2. Если кривая АС разбита на две части некоторой точкой В, то: 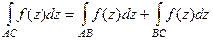
3. 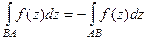 .
.
4. Если  то
то  , где
, где 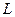 - длина кривой АВ.
- длина кривой АВ.
Пример. Вычислить интеграл 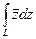 :
:
А) по прямолинейному отрезку от 0 до 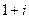 .
.
Б) по параболе от 0 до 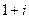 .
.
Решение.
А) 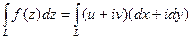 =
= 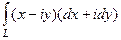 =
=
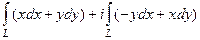 , далее вычисляем 2 криволинейных интеграла по отрезку, на котором
, далее вычисляем 2 криволинейных интеграла по отрезку, на котором 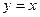 , заменяем
, заменяем 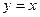 ,
,  .
.
При этом 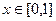 .
. 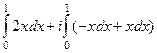 =
= 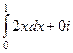 =
= 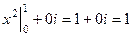 .
.
Б) Исходное раскрытие скобок происходит так же, как и в прошлом случае: 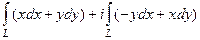 но теперь линия
но теперь линия 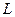 это не отрезок, заданный явным уравнением
это не отрезок, заданный явным уравнением 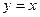 , а парабола, заданная явным уравнением
, а парабола, заданная явным уравнением 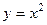 . Поэтому заменяем
. Поэтому заменяем 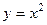 ,
, 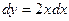 .
.
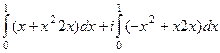 =
= 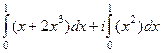 =
=
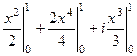 =
= 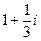 .
.
Ответ. по отрезку: 1, по параболе: 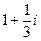 .
.
Как видим, в зависимости от формы кривой могут получиться разные ответы, но это здесь потому, что функция не аналитическая, она содержит 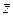 , а мы доказывали теорему 4 в конце прошлого § о том, что аналитичность равносильна отсутствию
, а мы доказывали теорему 4 в конце прошлого § о том, что аналитичность равносильна отсутствию 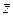 в составе функции, то есть тому, что
в составе функции, то есть тому, что 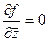 .
.
ЛЕКЦИЯ № 10. 17.03.2020
Вычислим интеграл от комплексной функции по замкнутому контуру.
Пример. Вычислить  , где
, где 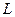 - окружность радиуса
- окружность радиуса 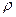 вокруг точки
вокруг точки 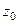 .
.
Решение.Представим функцию в виде 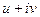 . Движение по такой окружности можно задать формулами:
. Движение по такой окружности можно задать формулами:
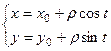
В этом случае 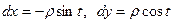 . Тогда
. Тогда
 =
= 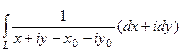 =
= 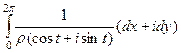 =
=
домножим на сопряжённое, 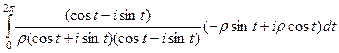 =
=
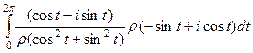 , можно сократить
, можно сократить 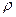 , а также вместо суммы квадратов sin и cos будет 1.
, а также вместо суммы квадратов sin и cos будет 1.
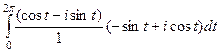 =
=
= 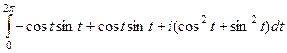 =
= 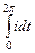 =
= 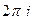 .
.
Теорема 1. Если 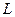 замкнутый контур, внутри которого во всех точках
замкнутый контур, внутри которого во всех точках 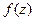 является аналитической, то
является аналитической, то  .
.
Доказательство. 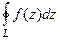 =
= 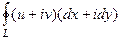 =
=
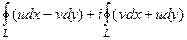 в двух этих интегралах - циркуляция двух векторных полей
в двух этих интегралах - циркуляция двух векторных полей  и
и 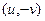 , они потенциальны по теореме 2 прошлого §, а тогда циркуляция равна 0, то есть получаем
, они потенциальны по теореме 2 прошлого §, а тогда циркуляция равна 0, то есть получаем 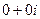 .
.
Теорема 2. Если 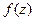 является аналитической во всех точках некоторой области
является аналитической во всех точках некоторой области 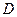 , граница которой односвязна, то интеграл от функции
, граница которой односвязна, то интеграл от функции 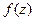 не зависит от пути, то есть имеет одно и то же значение для любой кривой
не зависит от пути, то есть имеет одно и то же значение для любой кривой 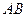 , соединяющей пару точек
, соединяющей пару точек 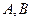 .
.
Доказательство.Аналогично прошлой теореме,
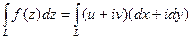 =
= 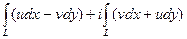 .
.
Криволинейные интегралы 2 рода от векторных полей  и
и 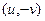 не зависят от пути, что доказано ранее в главе «теория поля».
не зависят от пути, что доказано ранее в главе «теория поля».
Так как для аналитической функции интеграл не зависит от пути, то для аналитической функции оказывается возможным ввести понятие первообразной. Введём в рассмотрение такую функцию: 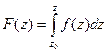 которая каждой точке ставит в соответствие интеграл до неё от некоторой фиксированной точки
которая каждой точке ставит в соответствие интеграл до неё от некоторой фиксированной точки 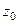 . Вводится по аналогии с вычислением потенциала поля, только в данном случае, вычисляются потенциалы двух полей
. Вводится по аналогии с вычислением потенциала поля, только в данном случае, вычисляются потенциалы двух полей  и
и 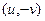 . Докажем, что построенная таким образом функция является первообразной.
. Докажем, что построенная таким образом функция является первообразной.
Теорема 3. Функция 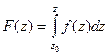 является первообразной от функции
является первообразной от функции 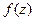 .
.
Идея доказательства.Докажем, что производная от 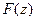 равна
равна 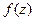 . По определению производной,
. По определению производной, 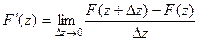 .
.
Распишем разность в числителе более подробно.
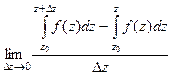 =
= 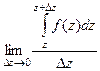 .
.
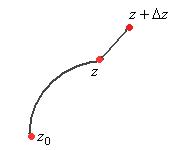
Интеграл в числителе можно представить с помощью значения в некоторой средней точке 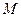 , расположенной между
, расположенной между 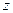 и
и 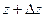 , так как интеграл от комплексной функции распадается на два криволинейных интеграла от потенциальных векторных полей.
, так как интеграл от комплексной функции распадается на два криволинейных интеграла от потенциальных векторных полей.
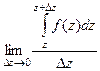 =
= 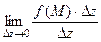 =
= 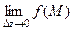 , причём при уменьшении
, причём при уменьшении 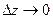 , точка
, точка  . Тогда
. Тогда 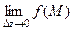 =
= 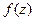 , что и требовалось доказать.
, что и требовалось доказать.
Примечание. Для потенциальных векторных полей верна теорема о среднем. Ведь для них интеграл не зависит от пути, и путь можно считать отрезком 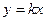 , тогда криволинейный интеграл сводится к
, тогда криволинейный интеграл сводится к 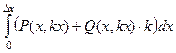 , где
, где 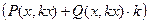 уже обычная скалярная функция, для которой верна теорема о среднем. Тогда существует некая точка
уже обычная скалярная функция, для которой верна теорема о среднем. Тогда существует некая точка 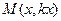 , так что криволинейный интеграл равен скалярному произведению
, так что криволинейный интеграл равен скалярному произведению 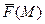 на вектор
на вектор 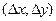 .
.
Итак, 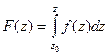 - вид первообразной от комплексной функции.
- вид первообразной от комплексной функции.
Теорема 4. Для функции, аналитической на кривой 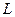 , верна формула Ньютона-Лейбница:
, верна формула Ньютона-Лейбница: 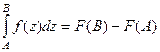 .
.
Доказательство.По построению первообразной,
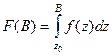 и
и 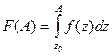 .
.
Но тогда 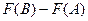 =
= 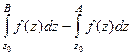 а тогда по 3-му свойству
а тогда по 3-му свойству
это 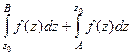 , что равно интегралу по кривой, проходящей от
, что равно интегралу по кривой, проходящей от 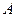 до
до 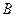 (через точку
(через точку 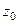 ).
).

Тогда 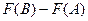 =
= 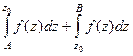 =
= 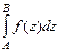 т.к. по свойству 2, их можно объединить. Итак,
т.к. по свойству 2, их можно объединить. Итак, 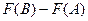 =
= 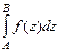 .
.
Пример. Вычислить 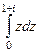 от 0 до
от 0 до 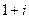 двумя способами:
двумя способами:
А) без формулы Б) по формуле Ньютона-Лейбница.
Решение.
А) 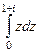 =
= 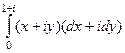 =
= 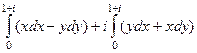
Пусть точки 0 и 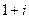 соединены по прямой
соединены по прямой 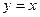 (вспомним, что интеграл не зависит от пути, поэтому можем соединить их как удобнее для вычислений). Тогда
(вспомним, что интеграл не зависит от пути, поэтому можем соединить их как удобнее для вычислений). Тогда 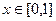 ,
,  , и
, и
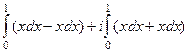 =
= 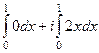 =
= 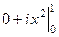 =
= 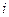 .
.
Б)По формуле: 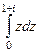 =
= 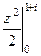 =
= 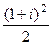 =
= 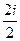 =
= 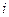 .
.
Дата добавления: 2020-03-21; просмотров: 878;











