Действия над матрицами.
Пусть в плоскости даны 2 вектора, каждый имеет по 2 координаты, тогда можно построить матрицу 2 порядка.
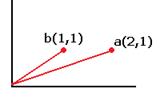
Матрица, соответствующая этой векторной системе 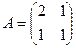 .
.
Аналогично, если дано 3 вектора в пространстве - можно построить матрицу 3 порядка.
Теперь рассмотрим произвольные матрицы.
Определение матрицы. Матрицей размера 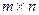 называется прямоугольная таблица, состоящая из чисел (либо других объектов, например, функций), содержащая m строк и n столбцов.
называется прямоугольная таблица, состоящая из чисел (либо других объектов, например, функций), содержащая m строк и n столбцов.
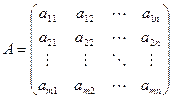
Каждый элемент обозначается 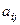 , где
, где 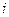 это номер строки, в которой он расположен, а
это номер строки, в которой он расположен, а 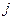 - номер столбца.
- номер столбца.
Обратите внимание: количество строк - это то же самое, что количество элементов в столбце, а количество столбцов равно количеству элементов в строке (заметим, что от каждого элемента 1-й строки начинается столбец, то есть сколько чисел в строке, столько и столбцов).
Если 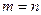 , то есть матрица А имеет размер
, то есть матрица А имеет размер 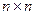 то она называется квадратной матрицей порядка n.
то она называется квадратной матрицей порядка n.
Примеры матриц из жизни:
1. Таблица результатов ЕГЭ по нескольким предметам в группе учеников.
2. Расписание занятий. День недели и номер пары, каждый элемент - номер аудитории в этот день в это время.
Сложение и вычитание матриц размера 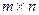 .
.
Эти операции определяются поэлементно, то есть суммируется или вычитается каждая соответствующая пара элементов 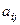 и
и 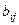 .
.
Пример: 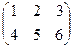 +
+ 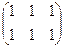 =
= 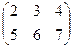 .
.
Умножение матрицы на константу определяется следующим образом. В матрице 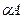 все элементы умножены на коэффициент
все элементы умножены на коэффициент 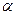 , то есть равны
, то есть равны 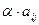 .
.
Транспонирование матрицы. Это довольно простая операция, и она вводится так. Если все пары элементов 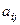 и
и 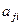 поменять местами, то получившаяся матрица называется транспонированной, она обозначается
поменять местами, то получившаяся матрица называется транспонированной, она обозначается 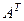 .
.
Дата добавления: 2020-12-11; просмотров: 583;











