Расчет аэродинамических подшипников. Источник несущей способности

Введение. Хотя теоретически аэродинамическая смазка отличается от гидродинамической, например вследствие влияния сжимаемости, практически любые различия в принципе действия часто проявляются лишь в различии названий. С точки зрения физических свойств аэродинамические подшипники могут отличаться от гидродинамических только по размерам, точности изготовления или по применяемым материалам, но форма подшипников обоих типов остается одинаковой.

Следовательно, анализ аэродинамических подшипников неизбежно имеет много общего с анализом гидродинамических подшипников, хотя часто внимание сосредоточивается на таких аспектах, как, например, точность соблюдения размеров и определение действующих нагрузок.

Прежде чем приступать к расчету аэродинамического подшипника, необходимо учесть многие факторы, которые можно разделить на шесть групп:
1) величина и изменение приложенных нагрузок;
2) величины параметров, влияющих на несущую способность и их изменение;

3) преимущества и недостатки различных типов аэродинамических подшипников;
4) несущая способность аэродинамических подшипников;
5) соотношение между ожидаемыми внешними нагрузками и расчетной несущей способностью;
6) относительные преимущества и недостатки по сравнению с аэростатическими подшипниками.

После краткого описания принципа действия аэродинамического подшипника, а также описания некоторых его практических свойств каждый из перечисленных факторов будет рассмотрен в отдельности.

Во многих случаях возможно выполнить точный и надежный расчет, но, как показано ниже, иногда вследствие недостатка исходных данных, например о внешних нагрузках или несущей способности, расчет аэродинамического подшипника первоначально основывается на интуиции, а затем подкрепляется последующим анализом.

Источник несущей способности. Хотя цель данной главы заключается в том, чтобы сосредоточить внимание читателя на практических сторонах расчета, тем не менее весьма полезно для понимания существа вопроса привести здесь краткое изложение основ теории, общих для аэродинамических подшипников различных форм. Сюда относятся простые цилиндрические радиальные подшипники и радиальные и упорные подшипники с самоустанавливающимися вкладышами. Исходные этапы теоретического анализа такие же, как и в теории гидродинамической смазки, и подробно описаны в соответствующих монографиях.

Чтобы слой смазки между находящимися в относительном движении поверхностями мог выдерживать нагрузку, необходимо уменьшать его толщину в направлении движения. В том, что такое уменьшение толщины приводит к повышению противодействующего нагрузке давления, можно убедиться с помощью следующего упрощенного рассуждения. Рассмотрим распределение скоростей по толщине пленки жидкости, текущей между двумя плоскими пластинами, в каждом из трех случаев, представленных на фиг. 2.1.

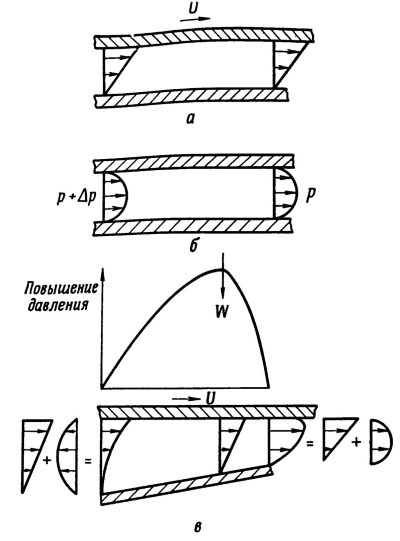
Рис. 2.1. Профили скоростей течения вязкой жидкости между двумя плоскими пластинами демонстрирующие причину возникновения повышенного давления в зазоре при наличии наклона и относительного движения пластин: а — течение, вызванное относительным движением; б — течение, вызванное перепадом давлений; в — комбинация течений

В случае а, когда пластины параллельны и одна из них перемещается относительно другой, распределение скоростей по толщине пленки линейно и давление вдоль пленки не меняется. Далее рассмотрим случай б, когда пластины параллельны, но неподвижны и течение жидкости порождается перепадом давлений. В этом случае распределение скоростей в зазоре между пластинами будет иметь параболическую форму. Наконец, проанализируем случай в, когда одна пластина наклонена и перемещается относительно другой. Для неразрывности потока необходимо, чтобы расход жидкости через подшипник был постоянным. Отсюда следует, что интеграл от распределения скоростей по толщине пленки должен быть одинаковым во всех точках.

Следовательно, форма кривых должна изменяться так, как показано на фиг. 2.1, в, т. е. при максимальной толщине пленки профиль скорости должен быть вогнутым, а при минимальной толщине — выпуклым. Итак, эти кривые приближенно можно представить как сумму линейного и порождаемого градиентом давления параболического распределения скоростей, откуда следует, что вдоль пленки в направлении движения должно иметь место изменение давления, подобно тому, как показано на фиг. 2.1, в, т. е. за первоначальным увеличением давления следует его снижение при подходе к сечению с минимальной толщиной пленки.

За счет этого автономного увеличения давления в зазоре между сходящимися поверхностями и возникает несущая способность большинства самогенерирующихся подшипников. Толщина смазочной пленки и наклон поверхности будут самоустанавливаться до тех пор, пока повышение давления не уравновесит приложенную нагрузку. Это положение принимается за основу при расчете любых самогенерирующихся подшипников и, в частности, аэродинамических. Итак, необходимо ответить на вопрос: какой минимальный зазор при заданной геометрии подшипника соответствует приложенной нагрузке?

Теоретический вывод уравнения для расчета повышения давления можно осуществить следующим образом. На фиг. 2.2 показан сходящийся клин, верхняя поверхность которого перемещается, а нижняя неподвижна. Ширина клина w в направлении, перпендикулярном плоскости ху, считается настолько большой, что течения в этом направлении не возникает, т. е. боковая утечка отсутствует. Предполагается далее, что течение ламинарное и в силу малой толщины пленки давление не зависит от у.

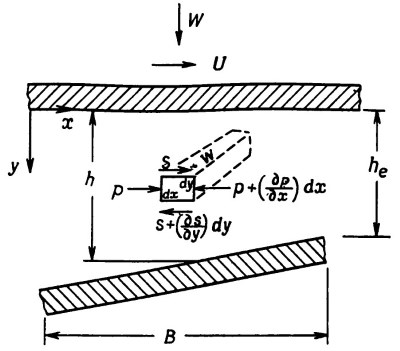
Рис. 2.2. Касательные и нормальные силы, действующие на элемент жидкости в пленке, имеющей форму сходящегося клина

Горизонтальные силы, действующие на малый элемент жидкости dxdy, обусловлены, во-первых, градиентом давлений в направлении оси х и, во-вторых, разностью касательных напряжений на верхней и нижней поверхностях элемента, обусловленных изменением скорости в направлении у. Условие равновесия этих сил будет иметь вид:

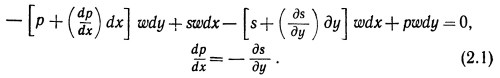
(Приращение касательного напряжения записано в виде частной производной, так как оно меняется как в направлении х, так и в направлении у.)

Касательное напряжение s пропорционально вязкости жидкости ц и градиенту скорости, т. е.

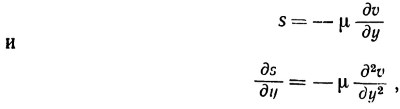
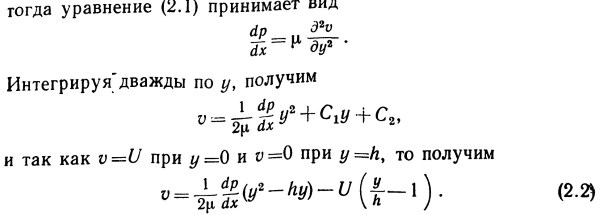
Отметим, что, как указывалось выше, это выражение для скорости представляет собой комбинацию параболического обусловленного градиентом давления распределения скорости и ее линейного распределения.

Масса жидкости, проходящей в единицу времени через любое течение, должна быть постоянной, т. е.

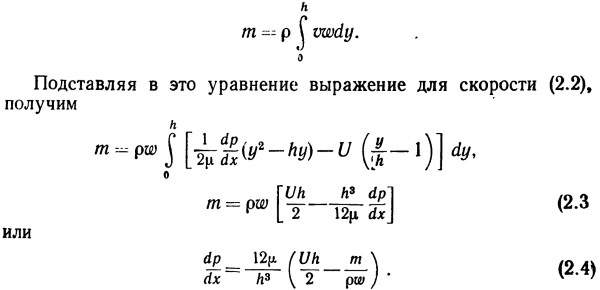
Для жидкостей плотность р постоянна, поэтому объемный расход на единицу ширины m/p не меняется. Итак, если зазор h (представляющий функцию от x) задан, то, проинтегрировав уравнение (2.4), можно получить распределение давления и несущую способность.