Расчет аэродинамических подшипников. Влияние сжимаемости

Уравнение (2.4) показывает также, что существующее различие между жидкой и газовой смазками сводится к различию между сжимаемой и несжимаемой жидкостями.

Поскольку газ сжимаем, его плотность не всегда постоянна, этому, если с увеличением давления плотность возрастает, отношение т/р будет уменьшаться и давление будет повышаться быстрее. Таким образом, форма кривых распределения давления в направлении движения для газовой и жидкой смазок не будет одинаковой (фиг. 2.3), и, следовательно, при наличии сжимаемости несущая способность также изменяется.

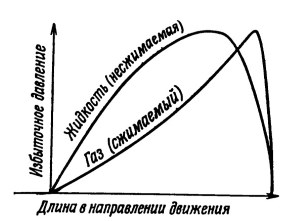
Рис. 2.3. Графическое сравнение распределения давления в подшипниках с несжимаемой и сжимаемой смазками

Влияние сжимаемости становится особенно заметным, когда изменение давления по длине подшипника в направлении движения велико по сравнению с внешним давлением. Если же изменение давления мало по сравнению с внешним, что имеет место в случае высоких давлений окружающей среды, то влияние сжимаемости пренебрежимо мало.

Это утверждение позволяет выявить значение давления среды, окружающей подшипник. Так, например, при малом внешнем давлении (меньшем нескольких атмосфер для 360-градусных радиальных подшипников) изменение последнего оказывает влияние на несущую способность, тогда как при большом внешнем давлении несущая способность не зависит от него (фиг. 2.4).

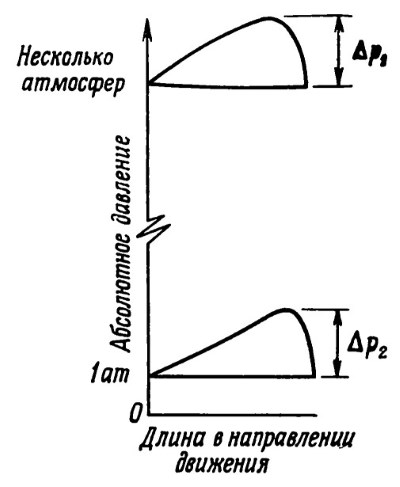
Рис. 2.4. Влияние окружающего давления на сжимаемость газовой смазки (при одной и той же нагрузке): Δ р₁ — изменение давления мало по сравнению с давлением окружающей среды, влияние сжимаемости пренебрежимо мало; Δр₂ — изменение давления велико по сравнению с давлением окружающей среды, влияние сжимаемости значительное

Как показал Пауэлл, процесс сжатия или расширения газа в подшипнике протекает по изотермическому закону. Таким образом, уравнение (2.3) можно переписать в виде

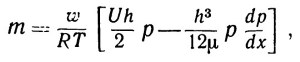
где R газовая постоянная, а Т — абсолютная температура газа.

При отсутствии боковой утечки масса газа в подшипнике будет оставаться постоянной в направлении х, т. е.

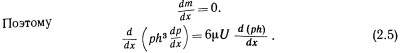
Это уравнение известно как дифференциальное уравнение Рейнольдса, описывающее распределение давления в сжимаемой смазке в случае, когда боковая утечка не учитывается.

Решение этого уравнения на практике усложняется, если, кроме сжимаемости, учитывать практическую геометрическую форму подшипника и влияние боковой утечки на несущую способность подшипника конечной длины. Некоторые приближенные решения для подшипников различной геометрической формы, полученные главным образом численными методами с помощью вычислительных машин, будут рассмотрены позднее; в этой связи следует обратить внимание на работы.

После выполнения интегрирований результат обычно имеет всегда одну и ту же общую форму как для радиальных, так и для упорных подшипников. Приведем два примера такой формы:

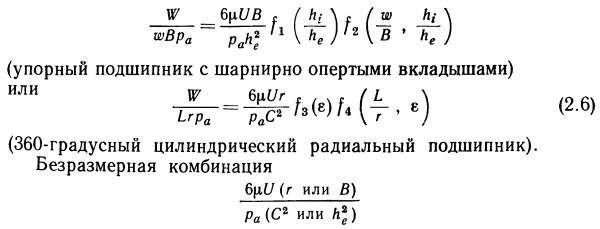
встречается наиболее часто. Эта комбинация называется числом сжимаемости и далее будет обозначаться буквой Λ, но в литературе встречаются и другие обозначения: Н, λ или G. Это число показывает, в какой степени сжимаемость влияет на работу подшипника. Например, из формулы (2.6) имеем

Если построить зависимость Р/р_а от Λ, степень ее отхода от прямой линии будет характеризовать влияние сжимаемости (фиг. 2.5).

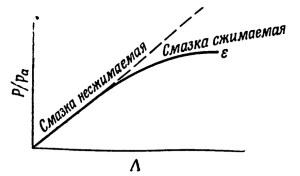
Рис. 2.5. Влияние сжимаемости на соотношение между Р/р_а и Λ

Практически для полного цилиндрического радиального подшипника при Λ<<1 смазка ведет себя как несжимаемая жидкость, а при Λ>>1 — как сжимаемая. В последнем случае, поскольку P/p_a не зависит от Λ, несущая способность подшипника становится не зависящей от скорости или вязкости. Эта тенденция к независимости несущей способности от скорости может иметь практическое значение и будет обсуждаться в разд. 2.4.