Переменный ток в активном сопротивлении. Мгновенная и активная мощность, действующее значение тока и напряжения
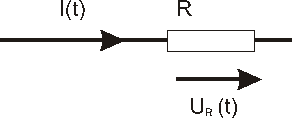
Пусть через активное сопротивление протекает синусоидальный ток:
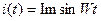
По закону Ома можно определить напряжение, возникающее на этом сопротивлении:
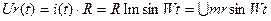
Как мы видим, фаза напряжения на активном сопротивлении совпадает с фазой тока, а амплитуда напряжения связана с амплитудой тока следующим соотношением:
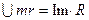 (1)
(1)
Как известно, при протекании через активное сопротивление тока, на нём выделяется энергия или совершается работа, характеризующаяся мощностью:


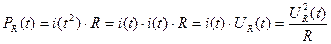
Эту мощность называют мгновенной мощностью и чаще всего определяют как произведение 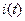 на
на 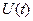 :
:
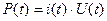
тогда 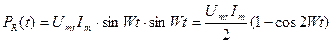
Эта мощность является функцией времени и имеет две составляющие.
Одна составляющая 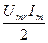 – постоянная, другая –
– постоянная, другая – 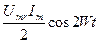 меняется с удвоенной частотой
меняется с удвоенной частотой 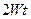 . Графики тока, напряжения и мгновенной мощности для активного сопротивления показаны на рис. 1.
. Графики тока, напряжения и мгновенной мощности для активного сопротивления показаны на рис. 1.
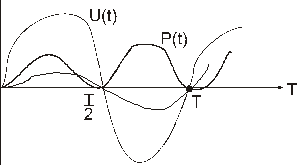
рис.1
Как видно из рисунка, мгновенная мощность активного сопротивления всегда положительна и меняется в пределах от 0 до 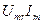 . Однако большинство электротехнических устройств обладают инерционностью. Например, мгновенная мощность бытовой лампы накаливания 100 раз в секунду принимает нулевое значение, однако температура её спирали так быстро меняться не может и остаётся практически постоянной. То же самое касается электроплитки и других электронагревательных устройств. Мгновенная мощность электродвигателя также меняется 100 раз в секунду, однако за счет инерционности вращения остается постоянной.
. Однако большинство электротехнических устройств обладают инерционностью. Например, мгновенная мощность бытовой лампы накаливания 100 раз в секунду принимает нулевое значение, однако температура её спирали так быстро меняться не может и остаётся практически постоянной. То же самое касается электроплитки и других электронагревательных устройств. Мгновенная мощность электродвигателя также меняется 100 раз в секунду, однако за счет инерционности вращения остается постоянной.
Таким образом, нас больше интересует не мгновенная мощность, а средняя мощность за определенный отрезок времени, в качестве которого чаще всего берётся период Т. Эта мощность называетсяактивной мощностью, для нахождения которой определим энергию, выделяющуюся за период Т, и поделим её на период Т:
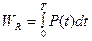
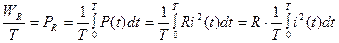 (2)
(2)
В данный момент уместно вспомнить аналогию с цепями постоянного тока, где мощность определялась как 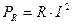 (3)
(3)
В цепях переменного синусоидального тока широко применяется понятие действующего значения, которое называют еще эффективным или среднеквадратичным. Сопоставляя формулы (2) и (3), получим выражение для действующего значения тока:
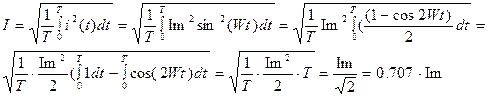
Действующее значение позволяет сопоставить работу синусоидального тока с работой постоянного тока, текущего то же время по тому же сопротивлению.
Аналогично можно вывести понятие действующего значения напряжения и ЭДС:
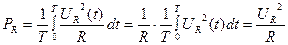 , где
, где
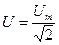 ,
, 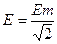
Таким образом, действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.
Пользуясь действующими значениями тока и напряжения, легко определить активную мощность сопротивления R:
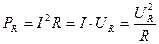
Действующие значения тока и напряжения связаны законом Ома: 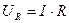 , что легко доказать, поделив левую и правую часть формулы (1) на
, что легко доказать, поделив левую и правую часть формулы (1) на 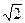
| <== предыдущая лекция | | | следующая лекция ==> |
| Активный и пассивный двухполюсники. | | | Коэффициент амплитуды и коэффициент формы |
Дата добавления: 2016-05-28; просмотров: 2166;











