Коэффициент амплитуды и коэффициент формы

Отношение амплитудного значения тока (или напряжения) к действующему называется коэффициентом амплитуды:

;

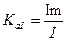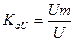
Для синусоидальных функций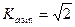

Отношение действующего значения тока (или напряжения) к среднему по модулю называется коэффициентом формы:

;

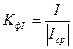Определим коэффициент формы для синусоидальной функции тока:

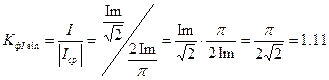
Для несинусоидальных периодических функций токов и напряжений 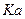и и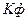меют другие значения.

Смысл коэффициента амплитуды вполне понятен: он связывает между собой амплитудное и действующее значение периодической функции. Измеряя ток или напряжение прибором электромагнитной системы, мы получим действующее значение и через 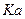найдём амплитуду. Сняв осциллограмму функции тока или напряжения, легко определить её амплитуду и через 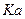найти действующее значение, необходимое для определения активной мощности.

В чем смысл коэффициента формы? Дело в том, что приборы электромагнитной системы имеют низкую чувствительность и малую точность, а приборы магнитоэлектрической системы показывают только постоянную составляющую, которая у синусоидальных функций равна нулю (среднее значение функции за период). Однако если включить такой прибор через выпрямитель (диодный мост), то он будет показывать среднее по модулю значение функции, которое связано с действующим значением через .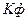

Очень часто детекторные приборы магнитоэлектрической системы градуируют в действующих значениях, хотя реагируют они на среднее по модулю значение. При этом используется 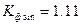(то есть прибор показывает 1А, а пишут 1.11А). Такой прибор правильно работает если им мерить синусоидальные функции, однако если форма тока будет несинусоидальной, то такой прибор будет давать заметную погрешность, обусловленную тем, что 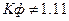, а прибор отградуирован именно под это значение. При этом чем сильнее форма функции отличается от синусоидальной, тем больше погрешность.