Простейшее понятие об информации (подход Хартли).
Будем считать, что если существует множество элементов и осуществляется выбор одного из них, то этим самым сообщается или генерируется определенное количество информации. Эта информация состоит в том, что если до выбора не было известно, какой элемент будет выбран, то после выбора это становится известным.
Найдем вид функции, связывающей количество информации, получаемой при выборе некоторого элемента из множества, с количеством элементов в этом множестве, т.е. с его мощностью. История науки не сохранила для нас вывода формулы для количества информации, предложенной Хартли. Поэтому в данной работе мы, стараясь следовать сложившейся традиции, попытаемся реконструировать его возможный ход мысли.
На качественном уровне его рассуждения могли выглядеть следующим образом.
Если множество элементов, из которых осуществляется выбор, состоит из одного-единственного элемента, то ясно, что его выбор предопределен, т.е. никакой неопределенности выбора нет. Таким образом, если мы узнаем, что выбран этот единственный элемент, то, очевидно, при этом мы не получаем никакой новой информации, т.е. получаем нулевое количество информации.
Если множество состоит из двух элементов, то неопределенность выбора минимальна. В этом случае минимально и количество информации, которое мы получаем, узнав, что совершен выбор одного из элементов. Минимальное количество информации получается при выборе одного из двух равновероятных вариантов. Это количество информации принято за единицу измерения и называется "бит".
Чем больше элементов в множестве, тем больше неопределенность выбора, тем больше информации мы получаем, узнав о том, какой выбран элемент.
На количественном уровне эти рассуждения могли бы иметь следующий вид.
Рассмотрим множество, состоящее из чисел в двоичной системе счисления длиной i двоичных разрядов. При этом каждый из разрядов может принимать значения только 0 и 1.
К ЭВРИСТИЧЕСКОМУ ВЫВОДУ ФОРМУЛЫ КОЛИЧЕСТВА ИНФОРМАЦИИ ПО ХАРТЛИ
| Кол-во двоичных разрядов (i) и кол-во состояний N, которое можно пронумеровать i-разрядными двоичными числами | Основание системы счисления и номера разрядов | |||||||||
| A | ||||||||||
| B | ||||||||||
| C | ||||||||||
| D | ||||||||||
| E | ||||||||||
| F | ||||||||||
| *** | *** | *** | *** | * | * | * | * | * | * | * |
Анализируя таблицу можно заметить, что при увеличении количества разрядов в двоичных числах на один количество состояний, которые можно пронумеровать с помощью этих чисел возрастает в два раза:
| Кол-во двоичных разрядов (i) | Кол-во состояний N, которое можно пронумеровать i-разрядными двоичными числами | |
| 4 | ||
| *** | *** | |
| i | 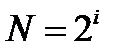
|
Аналогичное утверждение верно для чисел в любой системе счисления: при увеличении количества разрядов в числах в системе счисления с основанием E на один количество состояний, которые можно пронумеровать с помощью тих чисел возрастает в E раз. Например, при дописывании нуля к десятичному числу справа оно увеличивается в 10 раз, к двоичному – в два раза, к шестнадцатеричному – в 16 раз.
Итак, из таблицы видно, что количество этих чисел (элементов) в множестве равно:
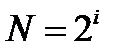
|
Рассмотрим процесс выбора чисел из рассмотренного множества. До выбора вероятность выбрать любое число одинакова. Существует объективная неопределенность в вопросе о том, какое число будет выбрано. Эта неопределенность тем больше, чем больше N – количество чисел в множестве, а чисел тем больше – чем больше разрядность i этих чисел.
Примем, что выбор одного числа дает нам следующее количество информации:
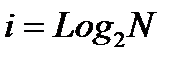
|
Таким образом, количество информации, содержащейся в двоичном числе, равно количеству двоичных разрядов в этом числе. Это количество информации i мы получаем, когда случайным равновероятным образом выпадает одно из двоичных чисел, записанных i разрядами, или из некоторого множества выбирается объект произвольной природы, пронумерованный этим числом (предполагается, что остальные объекты этого множества пронумерованы остальными числами и этим они и отличаются).
Это выражение и представляет собой формулу Хартли для количества информации. Отметим, что оно полностью совпадает с выражением для энтропии (по Больцману и Эшби), которая рассматривалась ими как количественная мера степени неопределенности состояния системы.
Сам Хартли, возможно, пришел к своей мере на основе эвристических соображений, подобных только что изложенным, но в настоящее время строго доказано, что логарифмическая мера для количества информации однозначно следует из этих двух постулированных им условий.
Дата добавления: 2016-06-22; просмотров: 2134;











