Мера Шеннона, как обобщение меры Хартли для неравновероятных событий.
Представим себе, что имеются объекты различных видов, причем:
– всего имеется M видов объектов;
– объектов каждого i-го вида имеется Ni:
Пусть, например, в мешке имеются бильярдные шары, на которых написаны числа 2, 4, 8 и имеется:
– 4 шара с надписью "2", т.е. N2=2;
– 4 шара с надписью "4", т.е. N4=4:
– 8 шаров с надписью "8", т.е. N8=8:
всего, 14 шаров.
Тогда по Хартли, если мы извлекаем один из объектов i-го вида, то получаем Ii бит информации
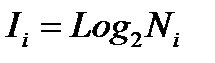
|
В частности:
– при извлечении шара с надписью "2" мы получаем 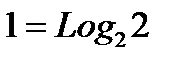 бит информации; бит информации;
|
– при извлечении шара с надписью "4" мы получаем 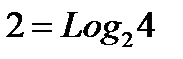 бит информации; бит информации;
|
– при извлечении шара с надписью "8" мы получаем 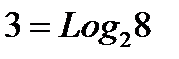 бит информации; бит информации;
|
В среднем по 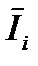 , т.е. на один объект i-го вида:
, т.е. на один объект i-го вида:
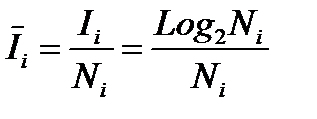
|
Или количественно в нашем примере:
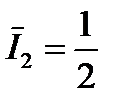
|
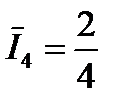
|
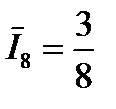
|
Сумма этих средних будет равна:
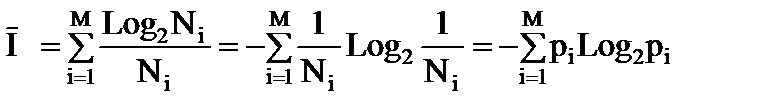
|
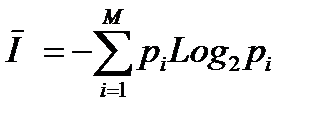
|
Последнее выражение – это и есть формула Шеннона, которая, таким образом, позволяет рассчитать средневзвешенное количество информации, приходящееся на один объект, получаемое при предъявлении объектов различных видов, причем внутри объектов каждого вида выбор равновероятен, а количество объектов разного вида вообще говоря различно.
При переходе от частот к вероятностям в формуле Шеннона использованы элементарные свойства логарифмов и введено обозначение: 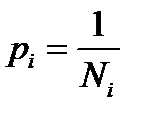 , которое традиционно интерпретируется как вероятность встречи объектов i-го вида.
, которое традиционно интерпретируется как вероятность встречи объектов i-го вида.
По мнению автора это не совсем точно, т.к. из элементарной теории вероятностей известно, что в общем случае вероятность определяется иначе, а именно как отношение количества событий определенного вида к общему количеству всех возможных событий всех видов.
Если использовать приведенные выше обозначения, то эта вероятность должна выражаться следующей формулой:
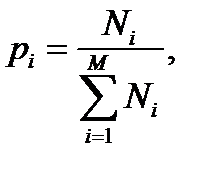
|
Из сравнения этих выражений видно, что общее выражение переходит в 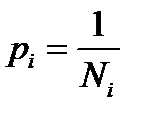 в случае, когда все Ni=1 и сумма всех Ni=N.
в случае, когда все Ni=1 и сумма всех Ni=N.
Количественно:
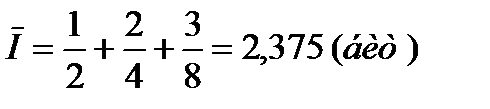
|
Если количество объектов каждого вида одинаково, то формула Шеннона преобразуется в формулу Хартли.
Отметим, что идентификация объектов, как относящихся к тому или иному виду (i-му виду) осуществляется на основе признаков этих объектов. В простейшем варианте это может быть и один признак, например номер вида на бильярдном шаре, но в реальных случаях признаков может быть очень много и их различные наборы сложным и неоднозначным образом могут быть связаны с принадлежностью объектов к тем или иным классам.
Но главный вывод от этого не изменяется: формула Шеннона дает средневзвешенное количество информации, приходящееся на один объект, получаемое при предъявлении объектов различных видов (классов), отличающихся своими наборами признаков. Мера Шеннона является обобщением меры Хартли для неравновероятных событий.
Дата добавления: 2016-06-22; просмотров: 2217;











