Перепишем теперь (1) в виде

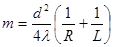, (4)

где d=BC – диаметр отверстия, R=SO, L=OM (см. рис. 2), l – длина волны.

Если d = 1 см, R = L= 10 см и l = 500 нм, то m = 1000. В этом случае А_m<<A₁ и слагаемым 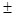А_m/2 в (3) можно пренебречь. Тогда, согласно (3),

А=А₁/2. (5)

Таким образом, амплитуда результирующей волны в точке Мопределяется как бы действием только половины центральной зоны Френеля. Ее диаметр d, как следует из (4) при m=1, R=L=10 см и l=500 нм, равен 0,32 мм.

Следовательно, распространение света от S к М происходит так, будто пучок света распространяется внутри очень узкого канала вдоль SM, т.е. прямолинейно.

В этом случае круговое пятно диаметром ED (см. рис. 2) равномерно освещено, и вне его наблюдается тень. Следовательно, дифракционная картина отсутствует, когда диаметр отверстия BC = d>>l.

При уменьшении диаметра отверстия до величины d 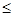1мм число зон согласно (4) уменьшается и А_m становится сравнимым с А_1, и поэтому пренебречь слагаемым 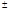А_m/2в (3) нельзя.

При нечетном числе зон, согласно (3),

А=А₁/2 +А_m/2 (6)

и в точке Мнаблюдается максимум (светлое пятно).

При четном числе зон

А=А₁/2 -А_m/2 (7)

и в точке М будет наблюдаться минимум (темное пятно). Этот факт особенно наглядно противоречит закону прямолинейного распространения света.

Очевидно, что максимум и минимум будут тем сильнее отличаться друг от друга, чем ближе значение А_m к А₁, т.е. когда число зон m мало (m 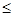10). Расчет амплитуды в других точках экрана более сложен. Можно показать, что дифракционная картина вблизи точки М имеет вид чередующихся темных и светлых колец с центрами в точке М. По мере удаления от точки Минтенсивность максимумов света убывает.

Если на пути световой волны в плоскости отверстия поставить зонную пластинку, которая перекрывала бы все четные зоны, то А=А₁+А₃+А₅+… и интенсивность I=A² в точке М резко возрастает. Еще большего эффекта можно достичь, не перекрывая четные зоны, а изменяя фазу их колебаний на p, тогда А=А₁+А₂+А₃+… Такая пластинка называется фазовой зонной пластинкой, и использование ее позволяет получить дополнительное увеличение интенсивности в 4 раза.

Опыт подтверждает эти выводы: зонная пластинка увеличивает интенсивность в точке М, действуя подобно собирающей линзе.

4.3.2. Дифракция Френеля на небольшом диске (круглом непрозрачном экране)

Способ построения зон Френеля на открытой части волнового фронта Ф падающей монохроматической волны показан на рис. 3. Пусть диск закрывает несколько зон, действие которых не будем учитывать. Нумерацию зон начнем от первой открытой зоны, расстояние до краев которой от точки М равны L и L+l/2. Последнюю открытую зону обозначим через m.

Проведя анализ, подобный предыдущему (см. 4.3.1), и полагая, что m достаточно велико, получим для амплитуды результирующей волны, выражение идентичное (5), т.е. А=А₁/2. Дифракционная картина на экране Э имеет вид концентрических темных и светлых колец с центром в точке М, где всегда находится максимум (пятно Пуассона).