Расчет электростатического поля двухпроводной заряженной линии в прямоугольном проводящем туннеле
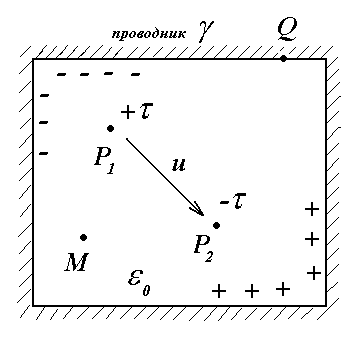
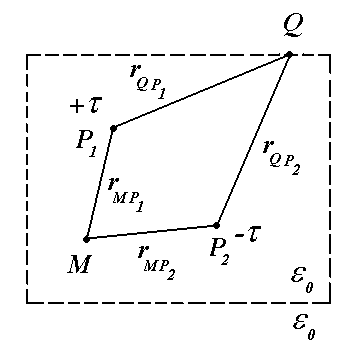
Дано: размеры поперечного сечения туннеля a , b ; положение в туннеле заряженных осей P1 , P2 .
Рассчитать: потенциал и напряженность электростатического поля в точке М
Решение
Потенциал ищется в виде наложения двух потенциалов
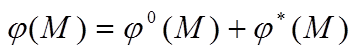 ,
,
потенциала в точке М от заряженной линии при отсутствии проводящего туннеля 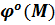 ипотенциала в точке М от индуцированных зарядов на поверхности проводящего туннеля .
ипотенциала в точке М от индуцированных зарядов на поверхности проводящего туннеля .
Так как туннель проводник, то на его поверхности потенциал результирующего поля постоянен и его можно принять равным нулю ( Q – точка на поверхности туннеля).
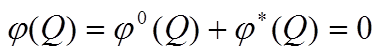
Следовательно
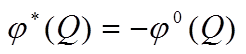
Потенциалы от заряженных осей (без учета индуцированных зарядов)
Потенциал на контуре следа туннеля
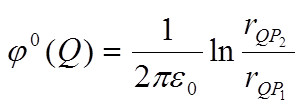
Потенциал в точке М
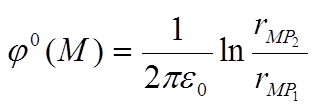
Для потенциала от индуцированных зарядов внутри туннеля будет справедливо уравнение Лапласа при заданном распределении этого потенциала на границе туннеля, то есть задача Дирихле.
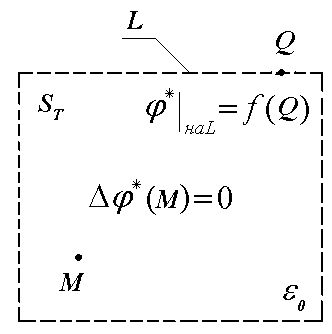
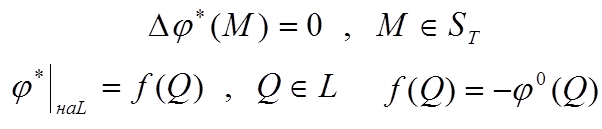
Решением уравнения Лапласа являются функции , обладающие такими свойствами:
-значение потенциала в точке М равно среднему от потенциалов точек окрестности.
-потенциалы точек внутри области не могут быть больше максимального
значения на границе области и меньше наименьшего граничного значения
Эти свойства определяются теоремами теории потенциала (из курса математической физики) :
-теоремой о среднем;
-теоремой о максимуме и миниуме.
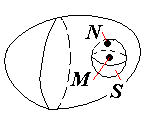
Теорема о среднем
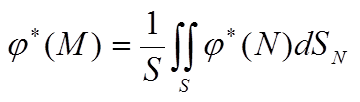
Теорема о максимуме и миниуме
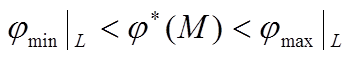
Свойства потенциала, полученные как решение уравнения Лапласа позволяют получать решение как аналитическими так и численными методами. Например, аналитически данная задача может быть решена методом разделения переменных. Среди численных методов можно отметить метод конечных элементов и метод сеток. Среди существующих математических пакетов прикладных программ в настоящее время можно выбрать необходимую для решения этой задачи.
Остановимся подробнее на численном методе сеток применительно к решению данной задачи Дирихле.
Для этого прямоугольную область (сечение туннеля) разбивают на ячейки (наносят сетку ) . В узлах сетки должны быть определены значения потенциалов.
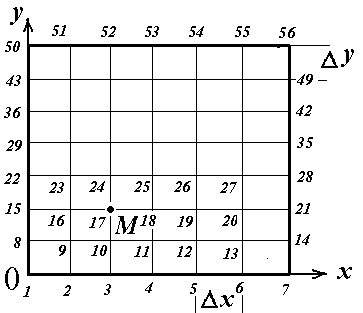
Номера узлов сетки в представленной декартовой системе координат пронумерованы от 1 до 100.
По теореме о среднем (по обозначениям рисунка)
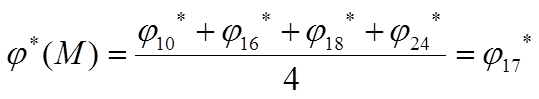
Метод сеток является итерационным методом последовательных приближений
при численном решении задачи Дирихле.
Решение начинается с произвольного задания значения потенциалов в узлах сетки, но эти значения не должны выходить за рамки максимального и минимального значений на границе туннеля в соответствии с теоремой о максимуме и миниуме потенциала. Далее проводится пересчет значений потенциалов в узлах сетки по вышеприведенной формуле. Значения потенциалов в узлах на границе туннеля при этом остаются неизменными .
Процесс пересчета потенциалов в узлах сетки называется итерациями. Из теории известно, что процесс итераций приближается к неизменяющемуся распределению потенциалов в узлах. Это установившееся распределение и является решением задачи Дирихле.
Количество итераций n определяется заданной по условию точностью расчета.
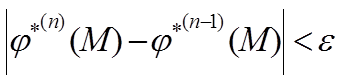
Пример 2
Дата добавления: 2020-03-21; просмотров: 814;











