Расчет поля в однородной среде по уравнениям Пуассона , Лапласа

<40 41 424344 45 46 >

Если требуется рассчитать поле в некоторой ограниченной поверхностью S части пространства с однородной средой, то необходимо знать распределение потенциала на этой поверхности. Потенциал внутри обьема V будет удоалетворять уравнению Пуассона (если в обьеме V есть распределеннные заряды) или уравнению Лапласа (если заряды в обьеме V отсутствуют).

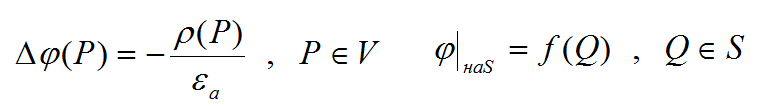
В курсе математической физике такие задачи называются краевые задачи.

Краевая задача с уравнением Лапласа называется краевая задача Дирихле.

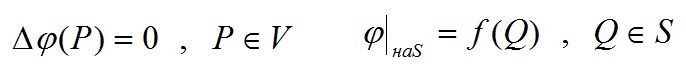
Если на границе области S задано распределение не потенциала, а а его нормальной производной 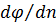, то эта задача носит название краевая задача Неймана.

Если область внутри обьема кусочно-однородна ( то есть состоит из диэлектрических однородных сред с различными значениями диэлектрических проницаемостей), то в краевой задаче необходимо ввести дополнительные граничные условия, учитывающие поведение векторов поля 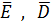на границе раздела этих сред

Представленные выражения означают равенство тангенциальных составляющих вектора напряженности электростатического поля и нормальных составляющих вектора электрического смещения ( электрической индукции) на границе сред 1 и 2.

<40 41 424344 45 46 >

Дата добавления: 2020-03-21; просмотров: 450;