Методы расчета нелинейных электрических цепей. Расчет схем с резистивными НЭ на постоянном токе

1. Аналитический

2. Линейной аппроксимации

3. Кусочно-линейной аппроксимации

4. Графический

5. Графо-аналитический

6. Численный

Аналитический метод расчета НЦ

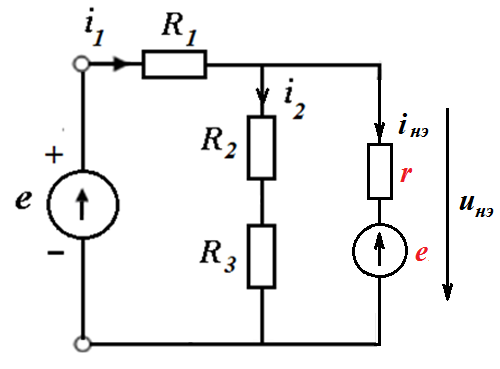
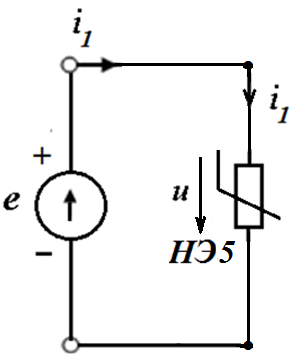
Суть аналитического метода заключается в составлении и решении нелинейной системы уравнений Кирхгофа. Нелинейные элементы при этом задаются своими ВАХ в виде математического (аналитического) выражения. Например, для ниже представленной цепи

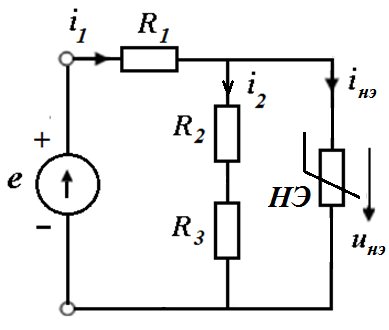
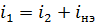
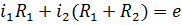
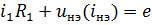
Если ВАХ НЭ представлчется в виде 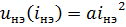, то система нелинейных алгебраических уравнений Кирхгофа сводится к одному квадратному уравнению относительно тока в НЭ i_нэ.

Метод линейной аппроксимации

Нелинейный элемент заменяется эквивалентным линейным сопротивлением. Для выще приведенной схемы с НЭ, ВАХ которого имеет вид 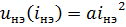ниже предсталена линейная аппроксимация НЭ сопроивлением R₀ .

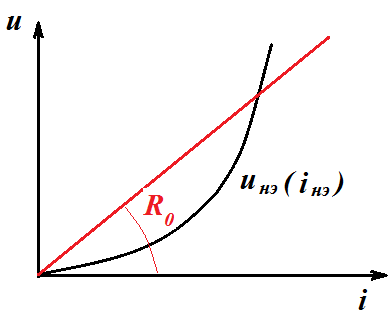
В этом случае 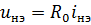и уравнения Кирхгофа становятся линейной системой алгебраических уравнений.

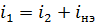
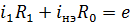
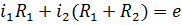
Решения этой линейной системы дает значения токов в ветвях цепи. Следует отметить, что точность результатов такого расчета может существенно отличаться от расчета исходной нелинейной цепи. Поэтому этот метод используется скорее для качестенной оценки процессов в цепях с НЭ.

Метод кусочно-линейной аппроксимации

При кусочно-линейной аппроксимации ВАХ НЭ участок линеаризации заменяется источником эдс 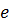с внутренним линейным сопротивлением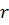

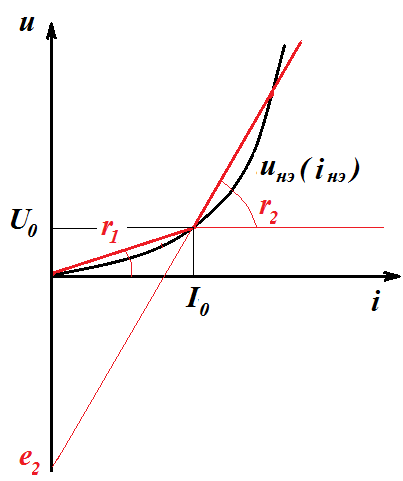
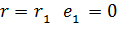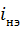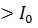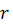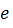На первом этапе расчета параметры участка линеаризации берутся равными: . Если после расчета получившейся линейной схемы окажется , то следует изменить параметры и на значения соответствующие второму участку линеаризации 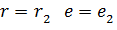. Затем расчет надо повторить

Графический метод расчета НЦ

Графический метод расчета применяется когда схема НЭЦ представляет собой комбинацию последовательно--параллельного соединения элементов.

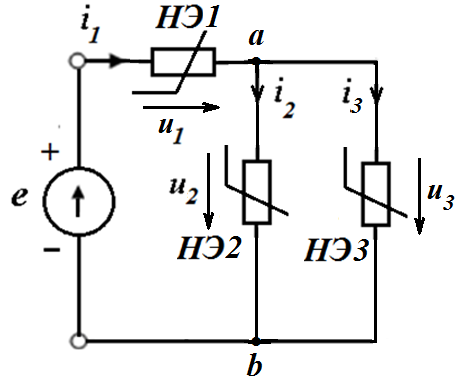
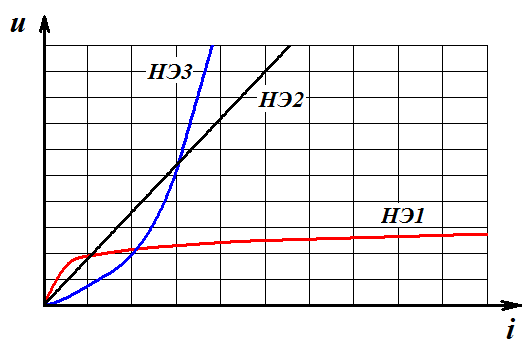
Заданы ВАХ НЭ1, НЭ2, НЭ3 Требуется рассчитать .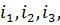

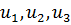НЭ2 и НЭ3 соединены параллельно, то есть напряжения 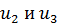одинаковы. ВАХ этих элементов можно сложить задаваясь рядом значений напряжений и, складывая соответствующие значения токов. В результате получится НЭ4 с ВАХ .

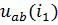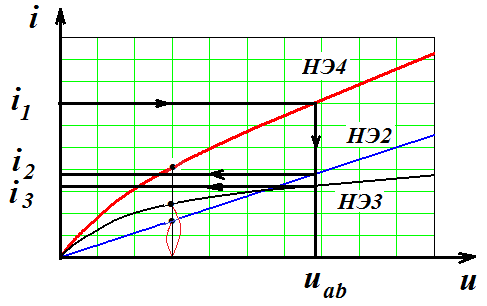
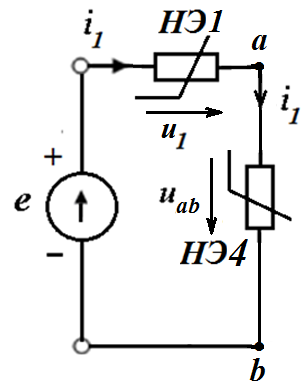
Далее НЭ1 и НЭ4 соединены последовательно с общим током 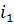. Их можно заменить эквивалентным НЭ5, который получится, если сложить НЭ1 и НЭ4, задаваясь рядом значений тока и, складывая соответствующие значения напряжений.

После проведенных графических построений расчет токов и напряжений проводится следующим образом. При заданном эдс становится известным напряжение на НЭ5. По ВАХ НЭ5 находится ток По току 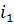и ВАХ НЭ4 находится напряжение 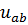. По напряжению 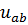и ВАХ НЭ2 и НЭ3 ищутся ток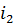и и .

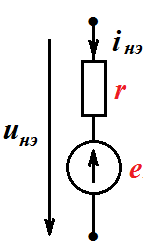
Графо-аналитический метод расчета НЦ

Графо-аналитический метод эффективен, когда схема содержит один НЭ. В этом случае линейная часть схемы заменяется эквивалентным генератором с параметрами .

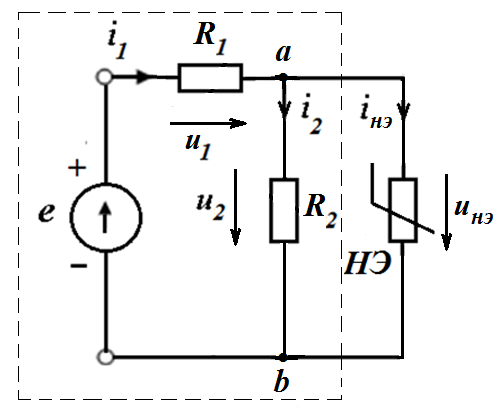
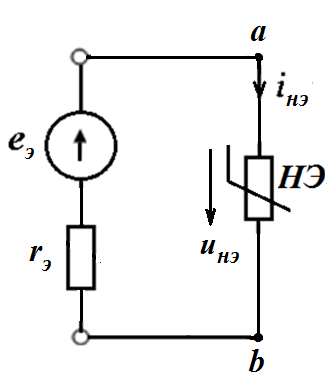
Для данной схемы параметры эквивалентного генератора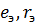

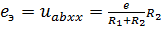
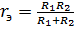
По второму закону Кирхгофа для эквивалентной схемы

.

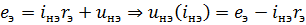Выражение в правой части называется внешняя характеристика ЭГ.

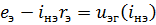
Графически внешняя характеристика ЭГ-это прямая линия. Решением является точка пересечения графиков НЭ и внешней характеристики ЭГ .

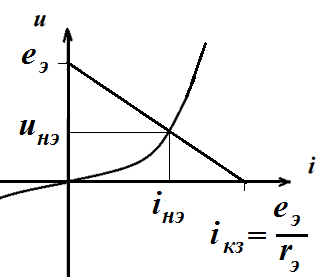
Численный расчет НЦ методом итераций

Суть численного метода заключается в том, что неизвестные значения токов или напряжений в НЭ на первом этапе расчета задаются как известные (нулевое приближение). Далее решается система уравнений Кирхгофа и находятся новые значения токов или напряжений в НЭ (первое приближение). Процесс пересчета (итерации) повторяется многократно (итерационный процесс) до установления повторяющихся значений токов в НЭ. В этом случае говорят, что итерации сходятся к решению. В курсе математики существует понятие критериев сходимости итерационного процесса. Сходимость зависит от выбора начального приближения и аргумента функции ВАХ .

Для большинства электротехнических нелинейных задач выполнение критерия сходимости связано с выпуклстью или вогнутостью вольт- амперных характеристик НЭ, то есть с монотонно убывающей или монотонно возрастающей производной вольт- амперной функции du/di . Если ВАХ НЭ имеет вогнутый характер, то в качестве начального приближения для НЭ следует брать напряжение на нем, если ВАХ НЭ имеет выпуклый характер характер, то в качестве начального приближения для НЭ следует брать ток в нем.

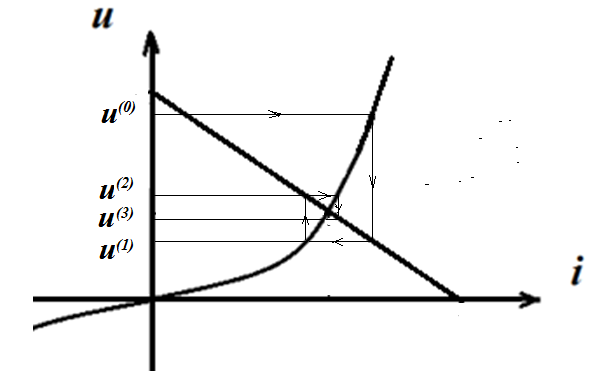
Вогнутый характер ВАХ НЭ, процесс итераций сходится к решению при задании начального приближения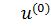

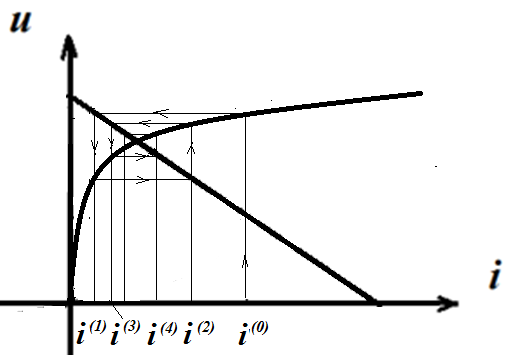
Выпуклый характер ВАХ НЭ, процесс итераций сходится к решению при задании начального приближения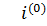

Если ВАХ НЭ имеют более сложный вид не монотонного характера и выполнение критериев сходимости проблематично можно использовать один из эффективных методов решения систем нелинейных алгебраических уравнений обеспечивающих сходимость итерационного процесса метод расщепления нелинейного уравнения. Суть метода расщепления в том, что из нелинейной части вычитается линейная часть, определяемая максимальным дифференциальным параметром ВАХ НЭ. Например, для цепи, изображенной ниже

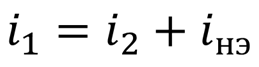
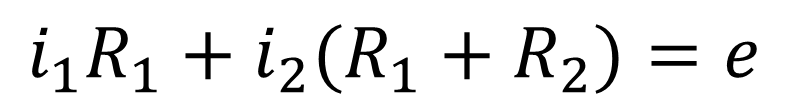
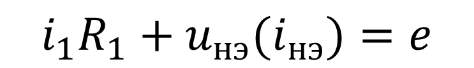
По методу расщепления вместо исходного нелинейного уравнения вводится уравнение

,

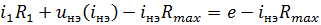которое записывается в виде

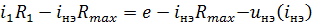
Тогда в матричной форме система уравнений Кирхгофа запишется в виде

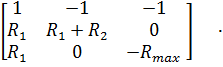
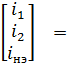
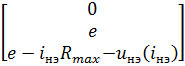
При таком подходе итерируется только правая часть, а матрица коэффициентов системы не изменяется, что обеспечивает минимальное время счета на ЭВМ и сходимость итераций к решению.