Методы контурных токов и узловых потенциалов.
На ранних этапах развития расчетных методов были созданы косвенные методы снижающие порядок решаемых уравнений Кирхгофа. Характерным для косвенных методов анализа является то, что в уравнениях, описывающих электромагнитное состояние ЭЦ, в качестве переменных подлежащих определению, выступают не искомые токи и напряжения, а некоторые вспомогательные величины, например, узловые потенциалы и контурные токи. Искомые токи и напряжения определяют по найденным узловым потенциалам и контурным токам с использованием законов Кирхгофа и Ома. Рассмотрим более подробно эти методы.
Метод контурных токов
Метод контурных токов (МКТ) является одним из основных косвенных методов расчета ЭЦ, который находит широкое применение на практике. Сущность этого метода заключается в том, что в каждом независимом контуре протекает свой условный, так называемый «контурный» ток. Система уравнений для контурных токов получается как результат сведения законов Кирхгофа к уравнениям только для независимых контуров. Уравнения для контурных токов составляются по известным правилам. Решение этих уравнений и определяет величину контурных токов. Действительный ток ветви находится как алгебраическая сумма контурных токов, протекающих в этой ветви.
Порядок расчета электрических цепей методом КТ
• Определяем независимые контуры и указываем направления отсчета контурных токов и действительных токов в ветвях .
• Определяем собственные, смежные сопротивления контуров и контурные эдс контуров.
• Составляем уравнения для контурных токов, используя стандартную форму записи этих уравнений. Решаем полученную систему уравнений и определяем контурные токи ЭЦ.
• Действительные токи определяются как алгебраическая сумма контурных токов, протекающих в этой ветви. При этом, если направление действительного тока совпадает с направлением контурного тока, то контурный ток берется с собственным знаком. В противном случае контурный ток берется с противоположным знаком
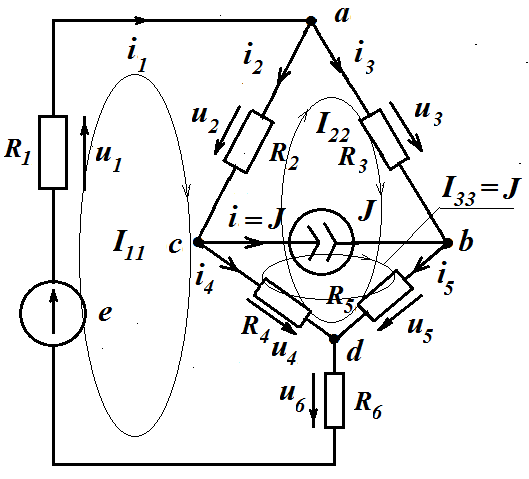
Рассмотрим ЭЦ, представленную на рис и произведем расчет этой ЭЦ методом КТ.
В схеме пять неизвестных токов ( i1 ,i2 ,i3 ,i4 ,i5 ), четыре узла ( a, b, c, d ) .
Независимых узлов- три (q-1=3),независимых контуров- два (5-3=2). На рис. в выбранных независимых контурах протекают два неизвестных контурных тока
I11 , I22 . .
Контурный ток I33 протекает через источник тока J ,его величина известна и равна току источника тока.
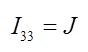
Составляем уравнения для контурных токов, используя стандартную форму
записи этих уравнений
. 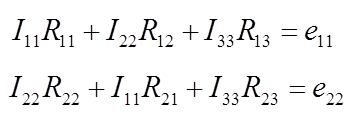
В этих уравнениях
R11 , R22 - собственные сопротивления контуров

R12 , R13 , R21 , R23 - смежные сопротивления контуров
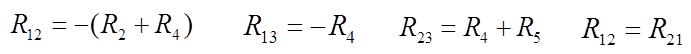
e11 , e22 - контурные ЭДС

Решение полученной системы алгебраических уравнений дает значение контурных токов
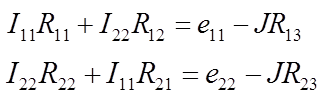
Токи в ветвях определяются через найденные контурные токи
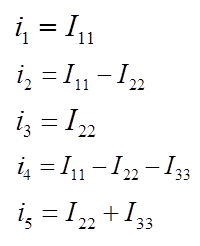
Метод узловых потенциалов
Методом узловых потенциалов называют метод анализа электрических цепей, в которых неизвестными являются потенциалы узлов ЭЦ.
Потенциал одного из узлов называемого базисным принимается равным нулю.
В качестве базисного узла схем обычно выбирают узел, в котором соединяется наибольшее количество элементов или, (при наличии в схеме идеальных источников напряжения) узел, с которым соединяется один из зажимов идеального источника напряжения.
Такой выбор базисного узла позволяет сократить число уравнений в системе, поскольку для узла, к которому подключен второй зажим источника напряжения потенциал оказывается равным ЭДС(со знаком + или - ), то есть оказывается известным.
Система уравнений для узловых потенциалов получается сведением системы уравнений Кирхгофа к уравнениям только для независимых узлов ЭЦ. Таким образом размерность решаемой системы уравнений уменьшается, что и является основным достоинством косвенных методов расчета ЭЦ.
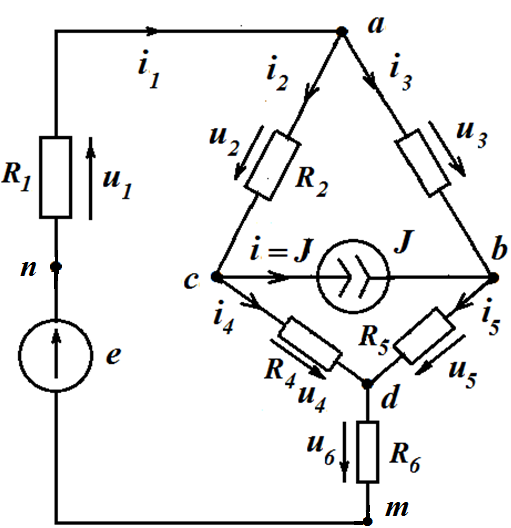
Рассмотрим ЭЦ, представленную на рис. и произведем расчет этой ЭЦ методом УП.
Для изображенной ниже схемы независимых узлов - 3. Следовательно , по МУП составляется 3 уравнения. В качестве базисного примем узел d
Система уравнений для узловых потенциалов имеет следующий вид:
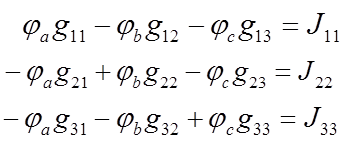
В этих уравнениях
g11, g22, g33 - собственные проводимости узлов
g11= 1/(R1+R6)+1/R2+1/R3 -проводимость узла а
g22= 1/R5+1/R3 -проводимость узла b
g33= 1/R2+1/R4 -проводимость узла c
смежные проводимости узлов
g12= 1/R3 -проводимость между узлами a и b
g13= 1/R2 -проводимость между узлами a и c
g23= 0 -проводимость между узлами b и c
J11, J22, J33 -узловые токи
J11=e/(R1+R6) -узловой ток узла a
J22 =J -узловой ток узла b
J33 =-J -узловой ток узла c
При использовании метода узловых потенциалов предлагается следующая последовательность решения задач.
1. Определение количества независимых узлов и выбор направлений отсчета искомых токов в ветвях.
2. Выбор базисного узла.
3. Составление системы уравнений для узловых потенциалов .
4. Определение собственных и смежных проводимостей узлов и узловых токов ЭЦ.
5. Решение системы линейных алгебраических уравнений и определение узловых потенциалов .
6. Расчет токов в ветвях ЭЦ с использованием рассчитанных узловых потенциалов и законов Кирхгофа и Ома.
Токи в ветвях схемы находятся через узловые напряжения по следующему мнемоническому правилу: ток в ветви равен разности узлового потенциала узла из которого он выходит минус узловой потенциал узла в который он входит , плюс э д с источника находящегося в этой ветви, если его стрелка совпадает со стрелкой тока или минус э д с источника , если его стрелка не совпадает со стрелкой тока и деленное на сопротивление ветви .
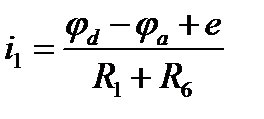 Например, для заданной ЭЦ ток i1равен
Например, для заданной ЭЦ ток i1равен
Дата добавления: 2020-03-21; просмотров: 923;











