Основные свойства и теоремы линейных электрических цепей.

В принципе, методом Крамера можно решить систему уравнений Кирхгофа для любой цепи постоянного тока, однако для расчета токов этот метод практически не используется. Вычисление определителей – это самый нерациональный по числу арифметических операций прием решения линейных алгебраических уравнений. Метод Крамера находит применение только в теории линейных систем, где он позволяет найти решение ряда задач в общем виде.

В теории электрических цепей разработаны более рациональные методы расчета токов, чем решение системы уравнений Кирхгофа. Однако, в тех случаях, когда исследуемая цепь не очень сложна, можно не заботиться о выборе рационального метода и решить систему уравнений Кирхгофа.

В общем случае решение системы уравнений Кирхгофа можно представить в следующем виде

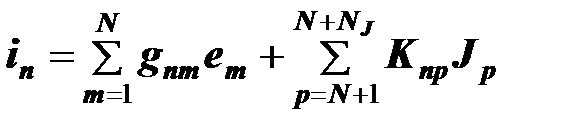
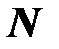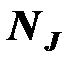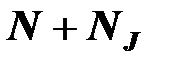Здесь - число ветвей электрической цепи, в которых протекают искомые токи ; - число источников тока в цепи, они имеют номера от до ; коэффициенты 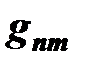и представляют собой отношения соответствующих алгебраических дополнений определителя системы к величине этого определителя. Значения этих коэффициентов зависят от сопротивлений и способа соединения элементов цепи. В первой сумме формулы необязательно содержится слагаемых; в некоторых ветвях может не быть источников ЭДС, в них равны нулю, и соответствующие им слагаемые также равны нулю.

Формула называется формальным решением системы уравнений Кирхгофа потому, что дает только общий вид решения. Нужно еще найти способ определения коэффициентов 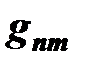и 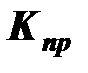. Вычисление этих коэффициентов через определители, которое было упомянуто выше, нерационально.

Входные и взаимные проводимости

Пусть в электрической цепи имеется один источник ЭДС и нет источников тока. Согласно формуле ток в любой ветви пропорционален ЭДС источника

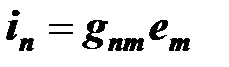
Предполагается, что источник включен в 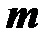-ю ветвь

Коэффициент пропорциональности между током -й ветви и ЭДС 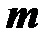-й ветви называется передаточной (взаимной) проводимостью между 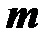-й и -й ветвями ( ).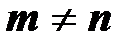

Если ток определяется в той же ветви, в которую включена ЭДС , то согласно формуле

Коэффициент пропорциональности между током 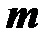-й ветви и ЭДС, включенной в эту ветвь, называется входной (собственной) проводимостью 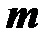-й ветви

.

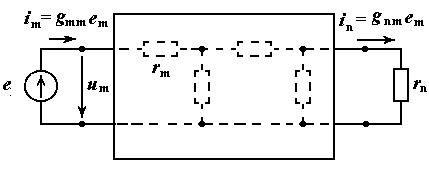
Передаточные коэффициенты по току

Пусть в электрической цепи имеется один источник тока и нет источников ЭДС. Согласно формуле, приведенной выше, ток в любой ветви пропорционален току идеального источника тока

.

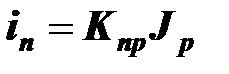Ветви с источником тока присвоен номер .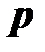

Коэффициент пропорциональности между током -й ветви и током идеального источника тока, включенного в 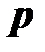-ю ветвь, называется передаточным коэффициентом по току между 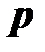-й и -й ветвями

.

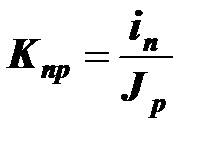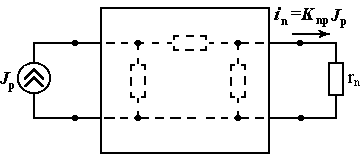
Определение передаточного коэффициента по току

Входные и взаимные проводимости, а также передаточные коэффициенты любой цепи могут быть выражены через определитель системы уравнений Кирхгофа и его алгебраические дополнения. Практически проще задать источник в одной ветви и, рассчитав токи в других ветвях, вычислить передаточные проводимости (или передаточные коэффициенты) с помощью их определений.