Информационная оценка качества фотоизображений.
Как отмечалось ранее, изображение представляет собой символ дифференциального плоского или объемного (одномерного или двумерного) ИВС, получаемый в результате отображения на фиксированный момент времени и на заданной ограниченной плоскости и зарегистрированный на некотором носителе. В дальнейшем при его обработке зарегистрированное изображение уже само может играть роль источника сообщения при информационном моделировании процессов его обработки.
Очевидно, что процессы отображения и регистрации изображения с точки зрения их информационных характеристик могут характеризоваться потерями информации, которые будут зависеть как от метода регистрации, так и от свойств носителя изображения. В настоящее время наиболее универсальным, быстродействующим и общепринятым методом регистрации оптических изображений является фоторегистрация, при котором изображение регистрируется (фиксируется) на светочувствительном фотоносителе в виде фотоизображения.
Фотоизображения очень часто используются в качестве источников визуальных сообщений в геодезии, картографии, исследовании природных ресурсов, экологии и других областях человеческой деятельности. Во многих из них информационную емкость фотоизображений определяют через их изобразительные и измерительные возможности применительно к решению какой-либо конкретной задачи. В этом случае, как правило, применяют семантический (субъективный) подход, так как оценивают количество информации с точки зрения возможности решения конкретной задачи (например, измерение или дешифрирование) при конкретной технологии использования фотоизображения. Кроме того, изобразительные и измерительные свойства фотоизображения определяются методами его получения, поэтому судить об информационных характеристиках самого фотоизображения не корректно.
С точки зрения теории информации более объективным является рассмотрение фотоизображения как источника визуальных сообщений, входящего в некоторую информационную модель, и оценка его предельных (потенциальных) возможностей с целью его информационного согласования с остальными блоками информационной модели.
Для примера рассмотрим черно-белое фотоизображение, которое, как известно, представляет собой дифференциальный одномерный плоский источник визуальных сообщений. В дальнейшем полученные выводы можно будет применить и к цветным фотоизображениям, которые являются дифференциальными двумерными плоскими источниками визуальных сообщений (см. рис. 4.5).
Согласно избранной модели (§4.2) источник визуальных сообщений можно разбить на элементарные площадки, причем, если размеры всех площадок одинаковы, то единица площади фотоизображения содержит N элементарных площадок:
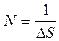 ,
,
где 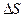 - площадь элементарной площадки.
- площадь элементарной площадки.
Положив, что возможные плотности почернения каждой площадки независимы, равновероятны и могут принимать одно из m значений, можно найти максимальное количество информации, содержащейся в единице площади фотоизображения (I),
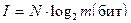 . (4.23)
. (4.23)
Применять это выражение для подсчета информационной емкости конкретного фотоизображения не корректно, так как конкретное фотоизображение имеет определенный закон распределения возможных плотностей элементарных площадок. Однако, при оценке максимально возможной информационной емкости, которая достигается при равновероятном распределении плотностей площадок, вполне допустимо. Затруднения при использовании этого выражения возникают при выборе m - числа возможных значений оптической плотности элементарных площадок, так как известно, что из-за своей природы фотоизображение немыслимо без наличия шумов, вызванных зернистостью фотослоя.
Наличие шумов ограничивает число различимых градаций плотности и тогда максимальная информационная емкость фотоизображения ( 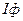 ), при условии равновероятности градаций плотности и их взаимной независимости, может быть определена по формуле Хартли:
), при условии равновероятности градаций плотности и их взаимной независимости, может быть определена по формуле Хартли:
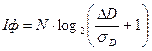 , (4.24)
, (4.24)
где 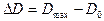 - диапазон возможного изменения оптической плотности;
- диапазон возможного изменения оптической плотности;
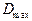 - максимально возможная плотность фотоносителя;
- максимально возможная плотность фотоносителя;
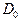 - плотность вуали;
- плотность вуали;
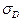 - среднеквадратическое значение шумов.
- среднеквадратическое значение шумов.
Формула (4.24) справедлива, если допустить, что сигнал и шум независимы и стационарны. Однако для фотоизображений эти допущения некорректны, так как известны эмпирическая зависимость, устанавливающая связь между средней оптической плотностью ( 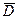 ) участка фотоизображения площадью (
) участка фотоизображения площадью ( 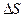 ) и среднеквадратическим значением флуктуации оптической плотности (
) и среднеквадратическим значением флуктуации оптической плотности ( 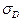 ):
):
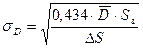 , (4.25)
, (4.25)
где 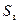 - средняя площадь проекции одного зерна используемого фотоматериала,
- средняя площадь проекции одного зерна используемого фотоматериала,
и выражение для определения соответствующего отношения сигнал/шум (y):
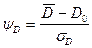 (4.26)
(4.26)
где D0 – плотность вуали.
 |  |
Графики зависимости
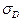 и
и 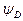 от
от 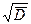 при
при 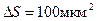 для различных фотоматериалов (1 – астропластинка; 2- панхром-10; 3 – панхром средней чувствительности; 4 – диапозитив; 5 – микрат-200; 6 – панхром мелкозернистая; 7 – кинопозитив МЗ) представлены на рис.4.9 и рис. 4.10 соответственно.
для различных фотоматериалов (1 – астропластинка; 2- панхром-10; 3 – панхром средней чувствительности; 4 – диапозитив; 5 – микрат-200; 6 – панхром мелкозернистая; 7 – кинопозитив МЗ) представлены на рис.4.9 и рис. 4.10 соответственно.
Рис.4.9 Графики зависимости 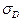 от
от 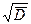 . Рис. 4.10 Графики зависимости
. Рис. 4.10 Графики зависимости 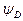 от
от 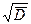 .
.
Анализ формул (4.24) и (4.25) показывает, что число различимых градаций будет функцией как средней оптической плотности ( 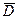 ), так и площади элементарной площадки (
), так и площади элементарной площадки ( 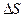 ), при изменения оптической плотности от
), при изменения оптической плотности от 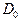 до
до 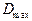 .
.
Найти в этом случае предельную  информационную емкость фотоизображения можно, разбив весь диапазон изменения плотности на L равноотстоящих уровней (и в дальнейшем устремив L к ∞), при этом разность между соседними уровнями равна
информационную емкость фотоизображения можно, разбив весь диапазон изменения плотности на L равноотстоящих уровней (и в дальнейшем устремив L к ∞), при этом разность между соседними уровнями равна 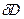
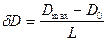 .
.
Средняя плотность элементарных площадок ( 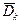 ), принадлежащих k-ому уровню, можно определить из выражения:
), принадлежащих k-ому уровню, можно определить из выражения:
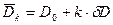 , (4.27)
, (4.27)
где 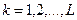 .
.
Число элементарных площадок ( 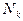 ) со средней плотностью
) со средней плотностью 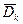 ,приходящихся на участок фотоизображения единичной площади, учитывая равновероятное распределение оптической плотности (для обеспечения максимального количества информации), может быть легко найдено:
,приходящихся на участок фотоизображения единичной площади, учитывая равновероятное распределение оптической плотности (для обеспечения максимального количества информации), может быть легко найдено:
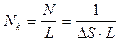 . (4.28)
. (4.28)
Из выражений (4.24), (4.25), (4.27) и (4.28) легко найти соотношение для нахождения максимального количества информации ( 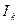 ), которое может содержать совокупность точек числом
), которое может содержать совокупность точек числом 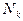 , принадлежащая k-ому уровню оптической плотности. Действительно,
, принадлежащая k-ому уровню оптической плотности. Действительно,
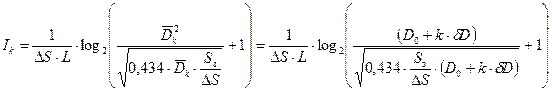 . (4.29)
. (4.29)
Общее количество информации, содержащееся в фотоизображении единичной площади ( 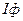 ), находится путем суммирования всех количеств информации (
), находится путем суммирования всех количеств информации ( 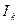 ), содержащихся в элементах разложения с плотностью
), содержащихся в элементах разложения с плотностью 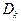 по k:
по k:
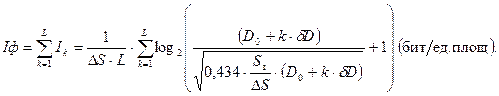 (4.30)
(4.30)
В полученном соотношении в качестве параметра используется L – число градаций по уровню оптической плотности. Представляет интерес зависимость предельного количества информации ( 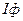 ) от избранного числа градаций оптической плотности (L). На рис.4.11 представлен график зависимости предельного количества информации, содержащегося на участке фотоизображения площадью 1 мм2, от числа градаций L при
) от избранного числа градаций оптической плотности (L). На рис.4.11 представлен график зависимости предельного количества информации, содержащегося на участке фотоизображения площадью 1 мм2, от числа градаций L при 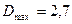 ,
, 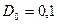 ,
, 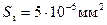 и
и 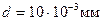 .
.

Рис. 4.11. График зависимости предельного количества информации, содержащегося на участке фотоизображения, от числа градаций L.
Таблица 4.3 содержит численные значения этой зависимости при некоторых заданных значениях L.
Табл.4.3
| L | ||||||||
| Iф(L)(бит) | 3,39·104 | 3,25·104 | 3,16·104 | 3,11·104 | 3,08·104 | 3,06·104 | 3,06·104 | 3,05·104 |
Из графика (Рис.4.11) видно, что в предельном случае, при 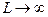 , можно найти точное предельное количество информации, содержащееся на участке фотоизображения заданной площади (
, можно найти точное предельное количество информации, содержащееся на участке фотоизображения заданной площади ( 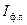 ). Для оценки погрешности вычисления предельного количества информации на участке фотоизображения построен график (Рис.4.12) зависимости отношения
). Для оценки погрешности вычисления предельного количества информации на участке фотоизображения построен график (Рис.4.12) зависимости отношения 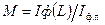 от числа градаций оптической плотности (L), при этом в качестве
от числа градаций оптической плотности (L), при этом в качестве 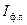 бралось
бралось 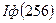 , а в Таблице 4.4 представлены численные значения отношения M при некоторых значениях L.
, а в Таблице 4.4 представлены численные значения отношения M при некоторых значениях L.

Рис. 4.12. График зависимости отношения 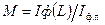 от числа градаций оптической плотности (L),
от числа градаций оптической плотности (L),
Табл. 4.4
| L | |||||||||
| M | 1,18 | 1,11 | 1,06 | 1,03 | 1,017 | 1,008 | 1,004 | 1,001 | 1,000 |
Из рис.4.12 и таблицы 4.4 видно, что для подсчета предельного количества информации, содержащейся на участке фотоизображения с погрешностью не превышающей 1%, число градаций оптической плотности должно быть не менее 32.
Пользуясь полученным выражением (4.30), можно рассчитать предельную информационную емкость некоего абстрактного фотоносителя как функцию площади элементарной площадки. Пусть фотоноситель имеет следующие параметры: 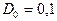 ;
; 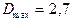 ;
; 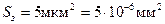 .
.
Выберем единицу площади фотоизображения 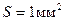 , а число уровней градаций оптической плотности
, а число уровней градаций оптической плотности 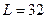 .
.
На рис.4.13 представлен график зависимости предельной информационной емкости фотоизображения площадью 1мм2 ( 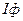 ) в зависимости от линейного размера элементарной площадки (d).
) в зависимости от линейного размера элементарной площадки (d).

Рис. 4.13. График зависимости предельной информационной емкости фотоизображения площадью 1мм2 ( 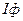 ) в зависимости от линейного размера элементарной площадки (d).
) в зависимости от линейного размера элементарной площадки (d).

А на рис.4.14 представлен график зависимости предельного среднего количества информации, приходящегося на одну элементарную площадку от линейных размеров элементарной площадки (d).
Рис.4.14. График зависимости предельного среднего количества информации, приходящегося на одну элементарную площадку от линейных размеров элементарной площадки (d).
В таблицу 4.5 сведены численные значения предельной информационной емкости участка изображения площадью 1мм2 ( 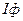 ), среднее количество информации, приходящееся на одну элементарную площадку (h) при различных линейных размерах (d) и площадях (
), среднее количество информации, приходящееся на одну элементарную площадку (h) при различных линейных размерах (d) и площадях ( 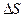 ) элементарной площадки.
) элементарной площадки.
Табл. 4.5
| d (10-3мм) | |||||||
| ΔS (10-6мм2) | |||||||
| Iф (бит/мм2) | 8,19·105 | 3,22·105 | 1,87·105 | 8,98·104 | 3,08·104 | 1,60·104 | 6,81·103 |
| h (бит/эл.пл.) | 0,82 | 1,33 | 1,70 | 2,24 | 3,08 | 3,60 | 4,26 |
Из таблицы 4.5 видно, что при линейных размерах элементарной площадки (d) менее 2 мкм среднее количество информации, приходящейся на одну элементарную площадку становится менее 1 бит, то есть число различимых уровней плотности элементарной площадки становится менее двух, что не позволяет различать отдельные элементарные площадки. Поэтому для рассмотренного фотоносителя использование элементарных площадок с линейными размерами (d) менее 2мкм нецелесообразно.
Сравнение данных Табл. 4.2 и Табл. 4.5 показывает, что информационная емкость оптического изображения единичной площади, приведенного в § 4.2, существенно выше информационной емкости фотоносителя такой же площади.
Представляет интерес определение зависимости относительных потерь информации, содержащейся на единичной площади оптического изображения, приведенного в Табл.4.2 при регистрации его на фотоносителе такой же площади (Табл.4.5), от линейных размеров элементарной площадки (d). В этом случае относительные потери информации 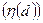 вычислялись по формуле:
вычислялись по формуле:
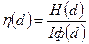 . (4.31)
. (4.31)
Результаты вычислений представлены в Табл. 4.6.
Табл.4.6
| d(10-3мм) | |||||
| h(d) | 3,66 | 2,34 | 2,01 | 1.87 | 1,76 |
Из этой таблицы видно, что зернистость фотоносителя особенно сильно влияет на относительные потери информации при малых линейных размерах элементарных площадок.
Следует заметить, что рассчитанная по формуле 4.30 информационная емкость фотоносителя является предельно возможной. Реальные фотоизображения обладают значительно меньшей информационной емкостью, так как их разрешение ограничено фотографическими системами, условиями съемки и обработки фотоматериала, а также достаточно произвольным распределением значений оптической плотности.
В случае, если известен конкретный закон распределения числа элементарных площадок ( 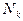 ), попадающих в каждый из L уровней плотности (гистограмма распределения) из выражения (4.30) может быть получено соотношение максимального количества информации (
), попадающих в каждый из L уровней плотности (гистограмма распределения) из выражения (4.30) может быть получено соотношение максимального количества информации ( 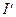 ), содержащейся на единичной площади такого изображения
), содержащейся на единичной площади такого изображения
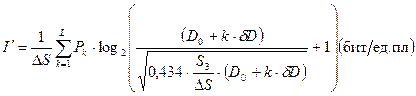 , (4.32)
, (4.32)
где 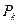 - вероятность попадания элементарных площадок в k-тый уровень оптической плотности.
- вероятность попадания элементарных площадок в k-тый уровень оптической плотности.
Следует подчеркнуть, что полученные соотношения (4.31) и (4.32) характеризуют фотоноситель только как носитель информации, в случае формирования оптического изображения, соответствующего заданному фотоизображению, необходимо учитывать и квантовые свойства источника света (§4.3).
Дата добавления: 2018-11-26; просмотров: 1075;











