Уравнения неразрывности.

· первой фазы 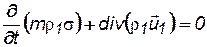; (5.7)

· второй фазы 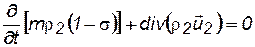. (5.8)

Если вытесняемая и вытесняющая фазы – слабосжимаемые упругие жидкости, то влиянием сжимаемости на распределение насыщенности можно пренебречь, так как время перераспределения давления за счет сжимаемости жидкостей, по крайней мере, на два порядка меньше, чем время вытеснения. Отсюда следует, что нестационарные процессы упругого перераспределения давления заканчиваются в начале процесса вытеснения. В некоторых случаях можно считать несжимаемым и газ в пластовых условиях.

Если жидкости и пористую среду можно предполагать несжимаемыми, то уравнения (5.7) и (5.8) упрощаются

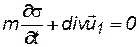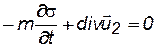, . (5.9)

Уравнения движения для многофазной фильтрации. При записи закона фильтрации предполагаем, что в любой точке каждая из фаз находится в термодинамическо - равновесном состоянии. Тогда для течения двухфазной смеси можно ввести в рассмотрение относительные проницаемости k_i(s) и капиллярное давление dр_к (s), зависящее только от насыщенности.

Кроме этого, рассматриваем только однонаправленные процессы фильтрации, не учитывая гистерезисных явлений. Тогда выполняется закон фильтрации (5.4):

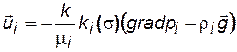, (5.10)

а связь между давлениями в фазах определяется равенствами (5.5) и (5.6):

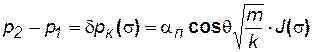. (5.11)

Для замыкания полученной системы уравнений необходимо задать дополнительные соотношения, рассмотренные в разделе 1 и связывающие параметры фаз и пористой среды с давлением.

Постановка и решение задач на основе полной системы уравнений фильтрации неоднородных жидкостей затруднительны ввиду сложности самих уравнений, а также формулировки краевых условий, в частности, разрыва капиллярных сил на границах пористой среды (так называемых концевых эффектов), роль которых недостаточно изучена.

Анализ одномерных двухфазных потоков позволяет выявить основные эффекты и характерные особенности совместной фильтрации жидкостей.