При нелинейном законе фильтрации

Если в некоторой области пласта с одномерным фильтрационным потоком действует нелинейный закон фильтрации, общее дифференциальное уравнение, описывающее движе-

ние, будет иметь иной вид, чем (IV.18)

Пусть, например, нелинейный закон фильтрации задан формулой.

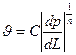, (IV.26,а)

Выражение массовой скорости фильтрации тогда можно записать так:

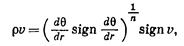
(IV.27)

и дифференциальное уравнение представится:

,

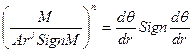где 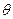— вспомогательная функция, определяемая следующим образом:

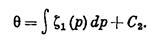
(IV.28)

Здесь С₂ — постоянная интегрирования, а 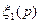выражает зависимость коэффициента С, взятого из формулы (IV.26,а), от давления р:

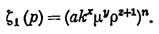
(IV.29)

Путем интегрирования дифференциального уравнения (IV.27)можно вычислить значение вспомогательной функции :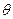

(IV.30)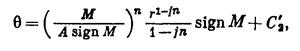

где 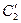— постоянная интегрирования; значения А приводятся в табл. 1.

При данных граничных условиях из (IV.30) найдем:

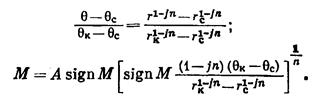
(IV.31)

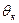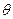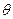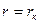Здесь и — значения при и 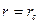соответственно. Если n = 1 (закон Дарси), значения функции 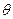выражают значения потенциальной функции 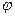и формулы (IV.21) совпадают соответственно с формулами (IV.22) и (IV.23).

Как уже указывалось, двучленные формулы типа (II.25) вернее отражают физическую сущность процесса, чем одночленные формулы. Выведем дифференциальное уравнение, основанное на двучленной формуле закона фильтрации, и покажем его решение.

Умножим все члены равенства (II.25) на 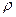и запишем его в дифференциальной форме применительно к простейшим видам одномерного потока:

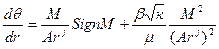, (IV.32)

где в данном случае вспомогательная функция

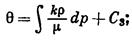
(IV.33)

где С₃ — постоянная интегрирования, остальные обозначения прежние.

После разделения переменных и интегрирования (IV.32) получим:

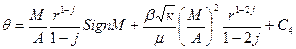, (IV.34)

где С₄ — новая постоянная интегрирования. При помощи граничных условий найдем:

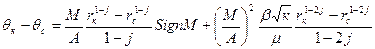.(IV.35)

Решая уравнение (IV.35) относительно М, найдем массовый дебит.