Для практики разведки и разработки пластов

В подземной гидравлике широко используются методы подземной гидрогазодинамики, являющейся разделом математической физики. Задачи одномерного потока относятся к классу краевых задач математической физики. Какова общая постановка такого рода задач?

Продуктивный пласт или выделенную из него часть можно рассматривать как некоторую область пространства, ограниченную поверхностями, сквозь которые либо происходит обмен жидкостью с внешней средой, либо обмена происходить не может ввиду их непроницаемости. В одном случае, например, этими граничными поверхностями пласта являются: контактная поверхность пласта с областью его питания (с дневной поверхностью, с естественным водоёмом); открытая стенка скважины, её забой. В другом случае граничную поверхность пласта представляет, например, непроницаемая для жидкости подошва — водоупор или граница пласта с непроницаемой породой, образовавшаяся вследствие тектонического нарушения (сброс).

Изучая перемещение жидкости в пласте, например приток её к забою скважины, мы рассматриваем движение в области, ограниченной соответствующими поверхностями.

Одномерным называется фильтрационный поток жидкости или газа, в котором скорость фильтрации, давление и другие характеристики течения являются функциями только одной координаты, отсчитываемой вдоль линии тока. Наиболее характерными, применительно к процессам фильтрации нефти, воды и газа, одномерными потоками являются:

прямолинейно-параллельный фильтрационный поток (параллельноструйный);

плоскорадиальный фильтрационный поток;

радиально-сферический фильтрационный поток.

Чтобы получить единственное решение задачи одномерного потока, надо иметь граничные условия, т. е. условия на граничных поверхностях пласта. Обычно ставится один из таких видов граничных условий: а) на определенных границах выделенной области пласта, например на забое скважины, давление задается постоянным; б) на одной граничной поверхности области пласта задаётся расход или скорость жидкости, на другой — давление.

Если заданы граничные условия, то, следовательно, нам известны местоположения граничных поверхностей, размеры пласта, местонахождение скважины. В такой постановке задача является прямой задачей подземной гидравлики.

Довольно часто, однако, на практике приходится сталкиваться с обратными задачами. В задачах этого типа неизвестными служат те или иные параметры пласта, его размеры, форма границ. Распре деление давления в пласте и дебит при этом должны быть заданы на основании промыслового наблюдения.

Рассмотрим простейшие виды одномерного течения жидкости, газа или их смеси в пласте.

1. Предположим, что в некоторой области пласта течение жидкости осуществляется так, что векторы скоростей её фильтрации во всех точках параллельны между собой. Тогда в этой области пласта будем иметь тот вид одномерного потока, который называется прямолинейно-параллельным.

Приведем некоторые примеры прямолинейно-параллельного потока.

Допустим, что нефтеводоносный пласт имеет в плане полосообразную форму (рис. 9, а). Мощность пласта мало изменяется вдоль протяжения, так что её можно считать везде одинаковой. Граничный контур пласта АВСDЕ непроницаем; он проходит по линии выклинивания или сбросового нарушения. Непроницаемы также кровля и подошва пласта. Батарея эксплуатационных скважин расположена параллельно начальному контуру нефтеносности ВD. На некотором удалении от батареи скважин поток жидкости будет практически прямолинейно-параллельным.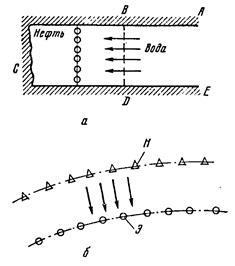

Рис. 9 Схема прямолинейно-параллельного потока жидкости в пласте полосообразной формы

Возьмём другой пример. Поток можно считать прямо линейно-параллельным на некотором участке между нагнетательной и эксплуатационной батареями сква-жин Н и Э (рис. 9, 6).

Относительно мощности пласта, его кровли и подошвы здесь сохраняются условия, оговоренные нами в предыдущем примере.

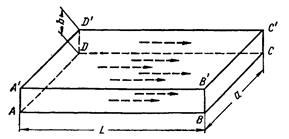
Для решения задач, относящихся к параллельноструйному течению жидкости в пласте, удобно представить себе модель, схематично изображающую пласт в виде прямоугольного параллелепипеда высотой b, которая здесь является мощностью пласта (рис. 10). Одна грань его 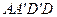служит границей пласта с областью питания, противоположная грань 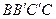является поверхностью стока. Можно вообразить, что поверхность стока ограничивает пласт от прямолинейной галереи длиной 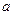, в которую стекает жидкость из пласта. 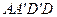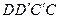Грани и непроницаемы для жидкости.

Грань 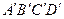изображает непроницаемую кровлю пласта, грань 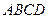— непроницаемую подошву. Фильтрация жидкости осуществляется по всей толще пласта, мощность которого равна b. Пунктирными стрелками показаны на рисунке векторы скоростей фильтрации.

2. Рассмотрим горизонтальный пласт неограниченной протяжённости, кровля А и подошва С которого непроницаемы (рис. 11, а). В пласте имеется единственная гидродинамически совершенная скважина. Гидродинамическое совершенство скважины определяется тем, что пласт вскрыт ею на всю мощность, скважина сообщается с продуктивным пластом через полностью

открытую для жидкости боковую поверх-Рис. 10. Схема параллельноструйного теченияность,отделяющую её ствол от продук-

жидкости в пласте.тивного пласта.

Кровля А и подошва С пласта параллельны друг другу.

На рис. 11, а изображена зона пласта, окружающая скважину 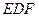. Через всю часть 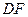стенки скважины может происходить обмен жидкостью между стволом и выделенной зоной пласта. На рис. 11, 6 показана та же зона в плане.

Если скважина 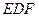— эксплуатационная, то жидкость притекает извне через боковую поверхность В выделенной зоны равномерно со всех сторон. Внутри зоны жидкость образует сходящийся радиальный поток (рис. 11, 6). Стоком жидкости является открытая боковая поверхность скважины .

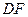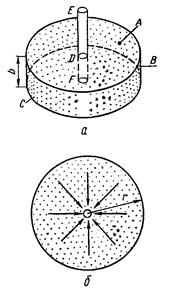Если 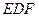— нагнетательная скважина, источником питания жидкостью выделенной зоны пласта служит стенка скважины 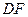, а стоком — боковая поверхность зоны В. Поток будет радиально-расходящийся.

При условии, что движение жидкости осуществляется в пределах всей мощности пласта - от его подошвы до кровли, -

рассматриваемое течение её может быть названо плоско-радиальным.

В плоско-радиальном потоке давление и скорость фильтрации зависят исключительно от расстояния частицы жидкости от скважины. Таким образом, этот поток является другим видом одномерного потока.

Рис. 11. Схема плоско-радиального потока жидкости в пласте.

В случае гидродинамически совершенной скважины плоско радиальным потоком можно считать тот, который возникает в так называемой призабойной зоне пласта, т. е. в ближайшей к скважине зоне.

З. Пусть в некоторой области пласта векторы скоростей фильтрации жидкости направлены вдоль пучка прямых, сходящихся в одной точке, причём давление и скорость фильтрации определяются исключительно расстоянием частицы жидкости от точки сход 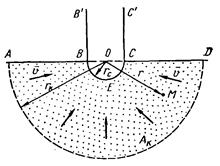а. Этот вид одномерного течения называется сферически-радиальным потоком. В условиях такого потока поверхностями равного давления (изобарами) и поверхностями равных скоростей (изотахами) являются сферические поверхности. Вообразим себе пласт неограниченной мощности с плоской непроницаемой горизонтальной кровлей АВСD, через которую скважина сообщается с пластом полусферическим забоем ВЕС (рис. 12).

Рис. 12. Схема сферически-радиального потока жидкости в пласте.

Течение жидкости в пласте по направлению к забою скважины или в обратную сторону является сферически-радиальным. К этому виду потока будет близок тот, который поддерживается в пласте очень большой мощности, имеющем горизонтальную непроницаемую кровлю, вскрытую скважиной, не углубившейся в пласт.