Потенциальное движение газированной жидкости

Газированная жидкость представляет собой смесь жидкой и газовой фаз. Газ находится не только в свободном состоянии; часть его растворена в жидком компоненте смеси.

В нефти, залегающей в естественных пластах, обычно содержится природный газ. Если давление в пласте выше давления насыщения нефти газом[3], весь газ растворяется в нефти, а нефть называется недонасыщенной. Задача об одномерном потоке такой нефти относится к тем, которые описаны в § б этой главы.

Если же пластовое давление ниже давления насыщения, то в процессе движения нефти в пласте из неё выделяется газ, находившийся в растворённом состоянии, и образуется движущаяся смесь нефти и свободного газа. Выделение газа из раствора обусловлено тем, что по пути фильтрации нефти давление снижается (так как движение направлено в сторону уменьшения давления).

Будем рассматривать движение каждой фазы в отдельности.

Различные эксперименты, проводившиеся по фильтрации двух- и трехфазной жидкости в пористой среде, показали следующее: проницаемость пористой среды для каждой фазы при движении её в составе смеси отличается от проницаемости, соответствующей случаю, когда через пористую среду фильтруется только один из данных компонентов смеси; принимается, что фазовые состояния компонента в потоке смеси и в однофазном потоке одинаковы.

Во всех экспериментах фазовая проницаемость образца пористой среды оказывалась меньшей проницаемости, определяемой пропусканием через образец однофазной жидкости. Это объясняется тем, что каждая фаза, входящая в состав смеси, как бы мешает движению другой фазы смеси. Чем больший относительный объём занимает компонент смеси в данной фазе, тем менее проницаем компонент в другой фазе той же смеси.

Во время движения в пласте газированной жидкости картина представляется такой: по мере продвижения смеси в направлении снижения давления из капельно-жидкого раствора (жидкого компонента смеси), выделяется все новая масса газа. Выделяющийся из раствора газ присоединяется к движущемуся свободному газу, вследствие чего увеличивается часть порового пространства, занимаемого газом. Свободный газ становится все более подвижным и фазовая проницаемость породы для газа растет, а фазовая проницаемость для жидкой фазы уменьшается. В одной и той же точке пористой среды фазовая проницаемость имеет, как правило, разные значения для жидкой и газовой фаз и находится в определенной зависимости от давления.

Предполагая неразрывность потока каждой фазы, расчеты дебита, давления и другие, относящиеся к потоку газированной жидкости, выполняют применительно к каждой из двух фаз смеси. Так, например, формулу (IV.18), выражающую массовую скорость фильтрации в одномерном потоке любой жидкости, можно применительно к капельно-жидкой фазе газированной жидкости записать так:

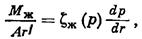(IV.42)

где М_ж — массовый дебит жидкой фазы; 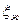— функция, определяемая для жидкой фазы формулой (IV.9), в которой величина k означает фазовую проницаемость.

В дальнейшем при выводе формул для фильтрации газированной жидкости ограничимся прямолинейно-параллельным и плоско-радиальным потоками.

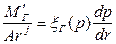Массовый дебит газового компонента смеси М_Г находится как сумма массового дебита газа, движущегося в свободном состоянии 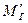и массового дебита газа, движущегося в растворенном состоянии 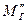. Используя формулу (IV.18) для свободного газа смеси, получим:

,(IV.43)

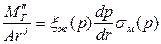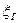где — функция (IV.9), в которой все величины 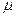и 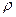относятся к газу; 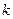— фазовая проницаемость.

Для газа, находящегося в растворе, найдем , (IV.44)

где 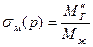есть массовая растворимость газа в жидкости, т. е. количество массы газа, растворенное в единице массы жидкости при давлении р.

Суммируя почленно равенства (IV.43) и (IV.44), получим:

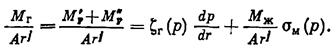(IV.45)

Для газированной жидкости пользуются при расчетах величиной объемного газового фактора G, который представляет собой отношение объёмного газового дебита 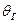, приведенного к давлению в 1 кгс/см² , к объёмному дебиту жидкого компонента 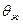‚ приведенному к тем же условиям. Поскольку, как было замечено в § 1 этой главы, массовый дебит на всех изобарических поверхностях в данном одномерном установившемся потоке один и тот же, сохраняется постоянным вдоль всего потока и газовый фактор G.

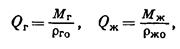Учитывая, что

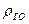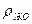где и — значения плотности газа и жидкого компонента соответственно, с помощью формул (IV.42) и (IV.45) получим:

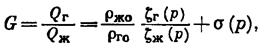(IV.46)

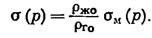где объемная растворимость газа в жидкости

(IV.47)

Если газ однороден, то в довольно широких пределах (примерно от 1 до 100 кгс/см² объемная растворимость пропорциональна давлению, т. е.

(IV.48)

где 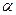— объёмный коэффициент растворимости, постоянный для данных жидкости и газа. Формула (IV.48) выражает закон Генри растворимости газа в жидкости.

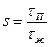Величина насыщенности жидкой фазой s показывает, какую часть данного объема порового пространства 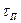, занимает жидкая фаза. Таким образом, имеем , где 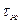— объём жидкой фазы. Газовая фаза занимает часть объема 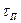, равную 1-s.

В результате экспериментов была найдена зависимость между относительной фазовой проницаемостью для жидкости и для газа 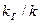и насыщенностью s, приведённая на рис.14.

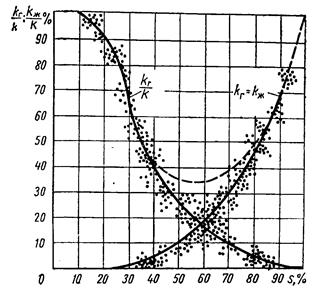Рис. 14. Зависимость относительных фазовых проницаемостей для газа и жидкости от насыщенности для несцементированных песков.

По кривым рис. 14 можно судить об особенностях фильтрации газированной жидкости. Так, при s = 80—90% = 48 — 70%; это означает, что присутствие в порах пласта от 10 до 20% свободного газа значительно снижает фазовую проницаемость для жидкой фазы. Фазовая же проницаемость для газовой фазы близка к нулю. Если s = 50% или ниже, то фазовая проницаемость для жидкой фазы = 8% или меньше.

При s = 20% = 0, т. е. жидкость не движется, а проницаемость для газа почти такая же, как если бы жидкости совсем не было. Если s>90%, то, как показывают экспериментальные и аналитические исследования, установившееся движение газированной жидкости невозможно. Насыщенность 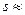90% называется равновесной насыщенностью. Заметим, что сумма

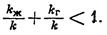
Следует учитывать, что в процессе разработки нефтяного месторождения при добыче попутного газа можно наблюдать такое явление: по мере снижения пластового давления совершенно прекращается отдача пластом нефти, а скважина дает чистый газ. Причиной этого может оказаться снижение насыщенности s до столь малой величины (s<20%), что фазовая проницаемость для нефти обращается в нуль; нефть, оставшаяся в пласте, не движется.

Решение задачи об одномерном потенциальном течении газированной жидкости строится в принципе по единой расчетной схеме, сущность которой выяснена в §6 настоящей главы. Следует прежде всего найти при помощи уравнения состояния выражения 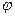в функции давления р, а затем использовать готовые формулы, беря граничные условия.

В формуле газового фактора (IV.46) функци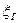и (р) и 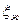(р) надо определять в соответствии с формулой (IУ.9). Тогда формула (IV.46) примет вид:

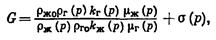(IV.49)

где (р) и 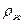(р) — плотность газа и жидкости соответственно.

В практических расчетах по технологии нефтедобычи учитывается величина объемного коэффициента нефти, зависящего от давления р. Объемный коэффициент нефти 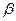(р) характеризует изменение объема нефти вследствие изменений давления и количества растворенного газа. Величина 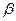(р) есть отношение удельных объемов нефти в пластовых и атмосферных условиях. Согласно данному определению

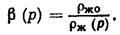
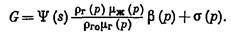Заменяя в формуле (IV.49) отношение функцией , получим 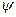(s):

(IV.50)

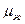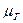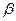При постоянном газовом факторе G уравнение (IV.50), выражая зависимость между давлением р и насыщенностью s, служит уравнением состояния газированной жидкости. Функции (р), (р), (р) и 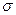(р) определяются по экспериментальным данным.

Уравнение (IV.50) решается относительно насыщенности s и полученное значение s подставляется в 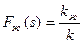или 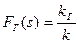Р, смотря по тому, движение какой фазы изучается — жидкой или газовой. Если значение s подставить, например, в 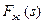, будем иметь следующий вид потенциальной функции 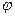(р):

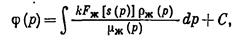(IV.51)

где s(р) — найденное из (IV.50) значение s в функции р.

Такова принципиальная схема решения задачи о фильтрации газированной жидкости.

Расчетные формулы для дебита по закону Дарси имеют наиболее простой вид, когда жидкость однородна и несжимаема. Такова, на пример, формула Дюпюи (IV.37) для объемного дебита. Придадим формуле для объемного дебита жидкой фазы газированной смеси в плоско-радиальном потоке вид формулы Дюпюи, сохранив в ней неизменным множитель .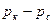

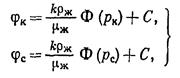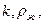Пусть и 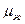- постоянны. Тогда из (IV.51):

(IV.52)

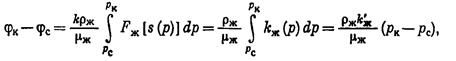где Ф (р_к) и Ф (р_с) — граничные значения интеграла вида 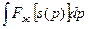. Вычитая почленно равенства (IV.52) и применяя известную теорему о среднем в интегральном исчислении, получим:

(IV.53)

где 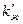- некоторое среднее значение функции 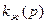в интервале изменения р от р_с до р_к.

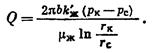Подставляя полученное значение 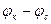% во вторую формулу (IV.25) и разделяя на постоянное 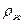найдем, что:

(IV.54)

Имеем явное сходство с формулой (IV.54).

Таким образом при расчете дебита жидкого компонента газированной жидкости можно использовать формулы для определения М или 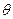‚ для однородной несжимаемой жидкости, если заменить в них проницаемость пласта 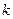некоторым средним значением фазовой проницаемости 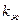. Другими словами — определить дебит газированной жидкости можно, заменив газированную жидкость воображаемой однородной несжимаемой жидкостью, движущейся в пласте с коэффициентном проницаемости 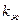, меньшим .

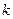На практике же дебит газированной жидкости при прочих равных условиях всегда меньше дебита однородной несжимаемой жидкости. С повышением газового фактора при неизменяющейся дпрессии 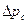дебит жидкой фазы уменьшается, а дебит газа увеличивается; при этом показатель 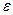растет, хотя и непропорционально G.

Глава V