Показатель формы потока

Во всех описанных в предыдущем параграфе случаях одномерного потока давление р, а следовательно, и потенциальная функция 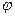, зависят только от одной координаты.

Если жидкость вытесняется из пласта через сток-галерею или сток-скважину, условимся принимать за координату произвольной точки пласта расстояние 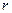до этой точки от: 1) стока-галереи (для прямолинейно-параллельного потока), 2) центра контура стока скважины в основной плоскости фильтрации (для плоско-радиального потока) и 3) центра полусферического забоя стока-скважины (для сферически-радиального потока). На модели прямолинейно параллельного потока, изображенной на рис. 10, расстояние 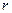от считывается таким образом от поверхности ВВ’С’С. На рис. 11, а расстояние 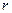берётся от точки F, если за основную плоскость течения принята подстилающая плоскость пласта С. На рис. 12 расстояние г отсчитывается от точки О схода всех векторов скоростей фильтрации.

Если жидкость внедряется в пласт через источник-галерею или источник-нагнетательную скважину, будем отсчитывать расстояние от источника-галереи или от соответствующего центра источника - скважины.

Каждый из трёх простейших видов одномерного потока позволяет считать, что пласт есть своего рода укрупнённая трубка тока и, значит, на всех изобарических (эквипотенциальных) поверхностях, определяемых уравнением 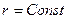, массовый дебит М — вели чина постоянная (см. § 1 настоящей главы). В данном случае вместо равенства (IV.2) следует записать: 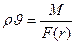, (IV.16)

где 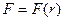— площадь эквипотенциальной поверхности в функции координаты 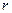. Отметим, что средняя скорость фильтрации на не которой эквипотенциальной поверхности совпадает в данном случае со скоростью фильтрации в любой точке этой поверхности.

Для прямолинейно-параллельного потока площадь F не зависит от координаты 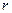и определяется так (см. рис. 10):

.

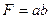Для радиальных потоков имеем указанные ниже значения площади изобарической поверхности:

Обратимся теперь к равенству (IV.7). В случае описанных здесь трёх простейших потоков оно представится так: 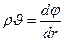.(IV.17)

Из (IV.17) видим, что положительной массовая скорость фильтрации будет в случаях, когда 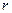отсчитывается от стока.

Приравнивая правые части равенства (IV.16) и (IV.17), получим общее дифференциальное уравнение трёх простейших видов потенциального одномерного потока:

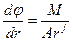, (IV.18)

где А и j имеют значения, указанные в табл. 1.

Таблица 1