Уравнения состояния жидкости, газа и пористой среды
Из предыдущего параграфа следует, что при установившемся течении жидкости для вычисления потенциальной функции 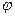 по формуле (IV.5) надо знать зависимость параметров
по формуле (IV.5) надо знать зависимость параметров 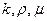 от давления р. При изотермическом процессе такая зависимость выражает состояние жидкости, газа или их смеси и пласта.
от давления р. При изотермическом процессе такая зависимость выражает состояние жидкости, газа или их смеси и пласта.
Зависимость определяется экспериментальным путем; плотность и вязкость жидкости (или газа), фазовая проницаемость породы, пропускающей сквозь свою толщу жидкость, записываются в функции от давления р.
Представим уравнение состояния в следующем виде:
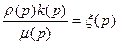 , (IV.9)
, (IV.9)
где 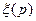 — подынтегральная функция в (IV.5).
— подынтегральная функция в (IV.5).
Если жидкость (или газ) однофазна и пласт однороден по проницаемости, множитель 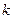 постоянен. Во многих задачах промысловой практики, кроме того, постоянным считают коэффициент вязкости
постоянен. Во многих задачах промысловой практики, кроме того, постоянным считают коэффициент вязкости 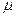 . Таким образом, если
. Таким образом, если 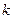 и
и 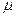 постоянные, уравнение состояния (IV.9) выражает зависимость между плотностью жидкости и давлением:
постоянные, уравнение состояния (IV.9) выражает зависимость между плотностью жидкости и давлением:
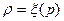 , (IV.10)
, (IV.10)
При изложении вопроса о фильтрации неоднофазной жидкости, например газированной нефти, будет рассмотрено соответствующее этому случаю уравнение состояния, получаемое с помощью экспериментальных данных. Теперь же рассмотрим уравнение (IV.9) применительно к некоторым другим частным случаям.
1. Пусть в пористой среде движется однородная несжимаемая жидкость. Тогда плотность остается постоянной и уравнение (IV.9) приобретает следующий вид:
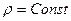 . (IV.11)
. (IV.11)
2. Предположим, что однородная капельная жидкость сжимаема и изменение её объёма происходит в соответствии с законом Гука. Мы можем воспользоваться величиной коэффициента объёмной упругости жидкости 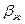 , который характеризует податливость жидкости изменению её объёма и показывает, на какую часть первоначального объема изменяется объём жидкости при изменении давления на единицу (если давление измеряется в кгс/см2 то на 1 кгс/см2
, который характеризует податливость жидкости изменению её объёма и показывает, на какую часть первоначального объема изменяется объём жидкости при изменении давления на единицу (если давление измеряется в кгс/см2 то на 1 кгс/см2
Основываясь на данном определении, напишем формулу для коэффициента объемной упругости жидкости:
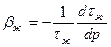 , (IV.12)
, (IV.12)
где 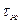 — объём жидкости; знак минус указывает на то, что объём увеличивается с уменьшением давления. Учитывая, что
— объём жидкости; знак минус указывает на то, что объём увеличивается с уменьшением давления. Учитывая, что
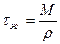 ,
, 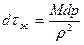 ,
,
где М — масса жидкости в объёме 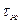 получим такое значение
получим такое значение 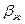 :
:
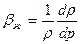 . (IV.13)
. (IV.13)
Зависимость (IV.13) и есть уравнение состояния капельной сжимаемой жидкости.
Его можно представить в конечной форме. для этого проинтегрируем (IV.13, получим
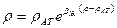 ,
,
где 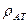 - плотность при атмосферном давлении РАТ, равном 1 кгс/см2
- плотность при атмосферном давлении РАТ, равном 1 кгс/см2
Величина 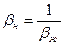 - называется модулем объёмной упругости жидкости. Коэффициент объёмной упругости нефти
- называется модулем объёмной упругости жидкости. Коэффициент объёмной упругости нефти 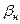 зависит от состава нефти; он изменяется с изменением давления и температуры и в значительной мере зависит от количества газа, растворенного в нефти. Коэффициент объёмной упругости негазированной (мёртвой) нефти изменяется в довольно узких пределах. По результатам лабораторных исследований пластовой нефти значения
зависит от состава нефти; он изменяется с изменением давления и температуры и в значительной мере зависит от количества газа, растворенного в нефти. Коэффициент объёмной упругости негазированной (мёртвой) нефти изменяется в довольно узких пределах. По результатам лабораторных исследований пластовой нефти значения 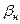 заключены в следующих пределах:
заключены в следующих пределах:
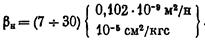
Во многих случаях допустимо принимать значение 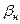 =10-4см2/кгс.
=10-4см2/кгс.
Коэффициент объёмной упругости воды 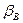 ‚ также изменяется в зависимости от давления, температуры и количества растворённого в воде газа, которое в свою очередь зависит от степени минерализации воды. Известно, что с увеличением давления уменьшается. При увеличении температуры до
‚ также изменяется в зависимости от давления, температуры и количества растворённого в воде газа, которое в свою очередь зависит от степени минерализации воды. Известно, что с увеличением давления уменьшается. При увеличении температуры до 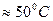 величина
величина 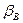 уменьшается; при дальнейшем увеличении температуры ‚ увеличивается (при не слишком больших давлениях). В некотором диапазоне давлений коэффициент можно считать постоянным. Можно наметить такие предельные значения коэффициента объёмной упругости воды:
уменьшается; при дальнейшем увеличении температуры ‚ увеличивается (при не слишком больших давлениях). В некотором диапазоне давлений коэффициент можно считать постоянным. Можно наметить такие предельные значения коэффициента объёмной упругости воды:
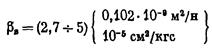
Часто берут значение
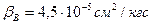 .
.
3. Выясним форму уравнения состояния газа.
Если газ идеальный, то при изотермическом процессе справедлив закон Бойля — Мариотта, который может быть записан так:
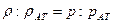 ,(IV.14)
,(IV.14)
это равенство выражает уравнение состояния идеального газа.
Для реальных газов пользуются уравнением Клапейрона, вводя поправку на сжатие и расширение газов при помощи коэффициента сжимаемости z:
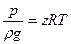 ,(IV.15)
,(IV.15)
где g — ускорение свободного падения; R — газовая постоянная; Т — абсолютная температура. Для одного моля газа R = 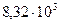 дж/град.кмоль.
дж/град.кмоль.
4. В начале этого параграфа было отмечено, что зависимость (IV.15) является уравнением состояния в случае установившегося течения и постоянной температуры. добавим, что то же уравнение используется и при неустановившейся фильтрации жидкости и газа в пористой среде.
Дата добавления: 2020-03-17; просмотров: 868;











