Термины и определения по надежности

Под надежностью элемента (системы) понимают его способность выполнять заданные функции с заданным качеством в течение некоторого промежутка времени в определённых условиях. Изменение состояния элемента (системы), которое влечёт за собой потерю указанного свойства, называется отказом.

Надёжность работы ВОЛП – это свойство волоконно-оптической линии обеспечивать возможность передачи требуемой информации с заданным качеством в течение определённого промежутка времени /1/.

ВОЛП в общем случае может рассматриваться как система, состоящая из двух совместно работающих сооружений – линейного и станционного. Каждое из этих сооружений при определении надёжности может рассматриваться как самостоятельная система.

В теории надёжности используются следующие понятия:

- отказ – повреждение ВОЛП с перерывом связи по одному, множеству или всем каналам связи;

- неисправность – повреждение, не вызывающее закрытия связи, характеризуемое состоянием линии, при котором значения одного или нескольких параметров не удовлетворяют заданным нормам;

- среднее время между отказами (наработка на отказ) – среднее время между отказами, выраженное в часах;

- среднее время восстановления связи – среднее время перерыва связи, выраженное в часах;

- интенсивность отказов – среднее число отказов в единицу времени (час);

- вероятность безотказной работы – вероятность того, что в заданный интервал времени не возникнет отказ;

- коэффициент готовности – вероятность нахождения линии передачи в исправном состоянии в произвольно выбранный момент времени;

- коэффициент простоя – вероятность нахождения линии передачи в состоянии отказа в произвольно выбранный момент времени.

Многоканальные ТКС относятся к восстанавливаемым системам, в которых отказы можно устранять.

Одно из центральных положений теории надёжности состоит в том, что отказы рассматривают в ней как случайные события. Интервал времени от момента включения элемента (системы) до его первого отказа является случайной величиной, называемой временем безотказной работы. Интегральная функция распределения этой случайной величины, представляющая собой вероятность того, что время безотказной работы будет менее t, обозначается q(t) и имеет смысл вероятности отказа на интервале (0… t). Вероятность противоположного события – безотказной работы на этом интервале – равна

P(t) = 1 – q(t).

Удобной мерой надёжности элементов и систем является интенсивность отказов l(t), представляющая собой условную плотность вероятности отказа в момент времени t, при условии, что до этого момента отказов не было. Между функциями l(t) и P(t) существует взаимосвязь:

P(t) = exp .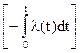

В период нормальной эксплуатации (после приработки, но ещё до того, как наступит физический износ) интенсивность отказов примерно постоянна l(t) » l. В этом случае

P(t) = exp (-lt).

Таким образом, постоянной интенсивности отказов, характерной для периода нормальной эксплуатации, соответствует экспоненциальное уменьшение вероятности безотказной работы с течением времени.

Среднее время безотказной работы находят как математическое ожидание случайной величины:

t_ср = l 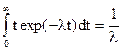. (7.1)

Оценим надёжность некоторой сложной системы, состоящей из множества разнотипных элементов. Пусть

P₁(t) ; P₂(t) ; … P_n(t) -

вероятности безотказной работы каждого элемента на интервале времени (0…t), n - число элементов в системе. Если отказы отдельных элементов происходят независимо, а отказ хотя бы одного элемента ведёт к отказу всей системы (такой вид соединения элементов называется последовательным), то вероятность безотказной работы системы в целом равна произведению вероятностей безотказной работы отдельных её элементов:

Р_сист = 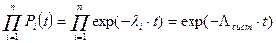. (7.2)

где L_сист = 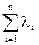— интенсивность от­казов системы;

l _i — интенсивность отказов i – го элемента.

Среднее время безотказной работы системы равно

t_{ср. сист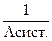} = . (7.3)

К числу основных характеристик надёжности восстанавливаемых элементов и систем относится коэффициент готовности:

К_г = 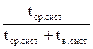, (7.4)

где t_{в сист} - среднее время восстановления элемента (системы).

Коэффициент готовности соответствует вероятности того, что элемент (система) будет работоспособен в любой момент времени.