Деформації елементів внаслідок втрати стійкості
Проаналізуємо напружений стан пластини при приварюванні ребер жорсткості (рисунок 9.10)
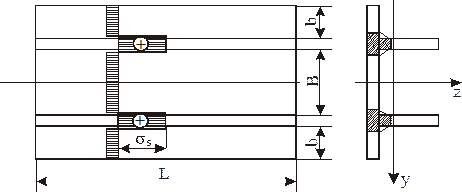
Рисунок 9.10 – Епюра напружень
Напруження у перерізах пластини від кожного шва визначаються за формулою
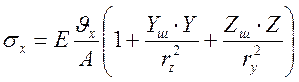 , (9.6)
, (9.6)
де 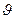 x- об’єм подовжнього укорочення, tі- деформації, відповідні границі текучості, rz, ry.- радіуси інерції перерізу площею A; Yш, Zш- координати шва в головних осях перерізу.
x- об’єм подовжнього укорочення, tі- деформації, відповідні границі текучості, rz, ry.- радіуси інерції перерізу площею A; Yш, Zш- координати шва в головних осях перерізу.
У даному випадку напруження у зонах термічного впливу напруження розтягуючі і дорівнюють границі текучості, у інших точках перерізу напруження
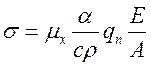 . (9.7)
. (9.7)
Ділянки пластини між ребрами жорсткості стиснуті напруженнями (9.7). Розрахункові схеми ділянок пластини можна розглядати як закріплені на бокових сторонах і навантажені зусиллями σ (рисунок 9.10).
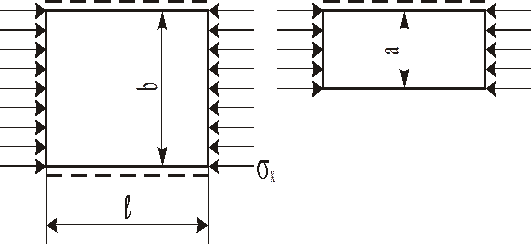
Рисунок 9.10 – Схеми пластин
Під дією стискаючих напружень пластини можуть втратити стійкість. Умова стійкості має вигляд
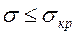 .
.
Критичні напруження визначаються за формулою ( 2 )
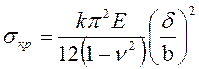 ,
,
де k - коефіцієнт, що залежить від співвідношення сторін l/b і закріплення кромок (таблиця 4.1); υ- коефіцієнт Пуассона (υ=0.3); δ, b- товщина і ширина пластини.
Якщо умова (9.8) не виконується, тобто 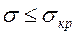 , пластина втрачає стійкість. Форма втрати стійкості близька дії синусоїди, причому довжина півхвилі l≈b для пластини, вільно закріпленої на двох сторонах і l=1.64b/2, для пластини з одним вільним краєм.
, пластина втрачає стійкість. Форма втрати стійкості близька дії синусоїди, причому довжина півхвилі l≈b для пластини, вільно закріпленої на двох сторонах і l=1.64b/2, для пластини з одним вільним краєм.
Таблиця 9.1 – Значення коефіцієнта k для стиснутої пластини
| Схема пластини | Відношення сторін a/b | |||||||||
| 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 3.0 | ||
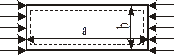
| 5.14 | 4.20 | 4.00 | 4.13 | 4.47 | 4.20 | 4.06 | 4.00 | 4.00 | 4.00 |
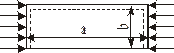
| 3.65 | 2.15 | 1.44 | 1.14 | 0.95 | 0.84 | 0.76 | 0.70 | 0.56 | 0.46 |
Прогин fт наближено можна визначити за формулою ( І )
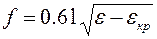 ,
,
де  .
.
Більш докладно питання втрати стійкості висвітлюється у [2].
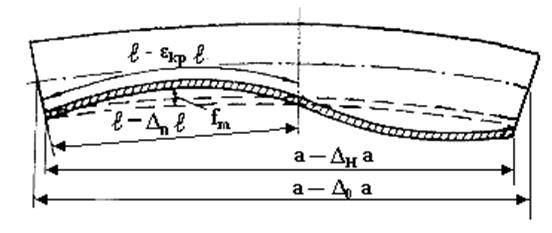
Рисунок 9.11 – Схема прогинів балки
Приклад 9.1 Пластини з маловуглецевої сталі зварюються автоматичним зварюванням під флюсом на режимі I=100A, U=30В, v=43м/год, η=0.8 двостороннім швом. Визначити кутові деформації і поперечний прогин, перевірити на стійкість зварене полотнище. Розміри пластин вказані на рисунку 9.12.
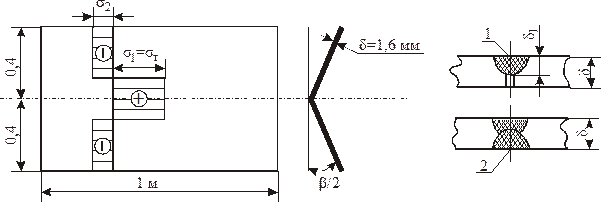
Рисунок 9.12 – Епюра напружень
1) Залишкові кутові деформації після виконання двостороннього шва визначаються сумою кутових деформацій від кожного із швів:
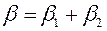
Для визначення β1 і β2 необхідно знайти глибину проникнення температури Т при наплавленні шва на лист наближено можна визначити за формулою:
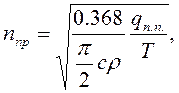
яка отримана у припущенні, що форма області обмеженої ізотермою Т по глибині – півкруг. У дійсності, ця форма суттєво залежить від способу зварювання, параметрів режиму, діаметра електродів і т.д. Особливо це стосується ізотерми T>0.2Tпл. У зв’язку з цим у більшості випадків глибина проплавлення визначається з використанням даних технологій зварювання.
Будемо вважати, що глибина проплавлення від одного шва складає 0.65δ, погонна енергія при v=1.2см/с:
 .
.
Питома погонна енергія
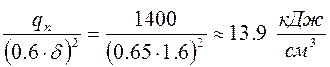 .
.
З графіка на рисунку 9.4 для швидкості зварювання v=1.2:
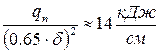 - одержимо
- одержимо 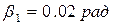 .
.
При визначенні кутової деформації розрахунковою товщиною у визначенні аргументу графіка 9.4 приймаємо повну товщину пластини.
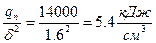
Кут повороту β2 згідно з рисунком 9.4, β2=0.017 рад.( мінус означає, що кут β2 протилежний куту β1 ).
Сумарний кут повороту буде у бік першого кута
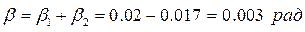
Поперечний прогин
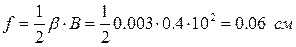 .
.
2. Для відповіді на питання, чи втратить пластина стійкість після зварювання, визначимо залишкові напруження у стиснутій частині площі поперечного перерізу і порівняємо їх з критичними.
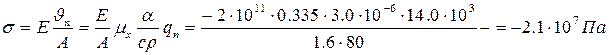 .
.
Критичні напруження визначаються за формулою
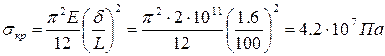
Оскільки 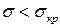 , втрати стійкості не відбудеться.
, втрати стійкості не відбудеться.
Приклад 9.2 Визначити місцеві деформації і перевірити на стійкість при зварюванні листа з двома ребрами жорсткості (рисунок 9.13). Матеріал – маловуглецева сталь 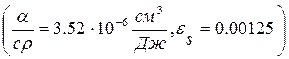 .
.
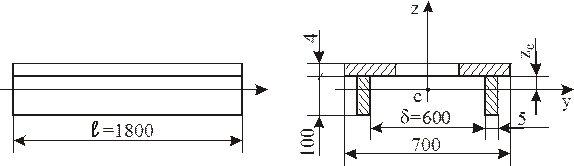
Рисунок 9.13 – Схема конструкції
Катет двосторонніх зварних швів К=4 мм. Погонна енергія:
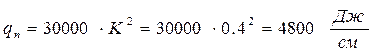 .
.
Координата центра ваги перерізу
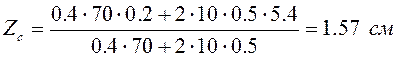 .
.
Момент інерції перерізу відносно осі Y
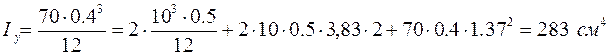 .
.
Напруження у перерізах, перпендикулярних ребрам жорсткості,
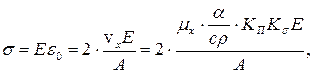
де КП – коефіцієнт, враховуючий перекриття пластичних зон сусідніх швів (рисунок 9.14) 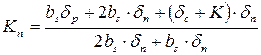 ;
;
Кσ – коефіцієнт, враховуючий вплив напруженого стану від попередніх швів на об’єм Vx шва. При раціональній послідовності виконання швів можна забезпечити відсутність прогинів конструкції відносно осі Z.
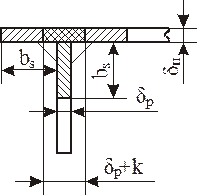
Рисунок 9.14 – Схема перекриття пластичних зон сусідніх швів
Визначимо розмір пластичної зони від одного шва
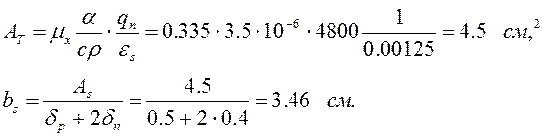
Коефіцієнт перекриття
 .
.
Напруження стиску у точках на осях X:
 .
.
Напруження у перерізах листа
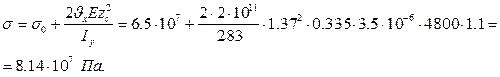
Якщо розглядати середню частину листа як пластину, закріплену на подовжніх ребрах, то критичні напруження знаходять за формулою
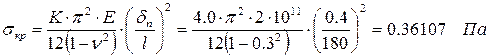
( k = 4.0 таблиця 9.1).
Діючі напруження більші критичних, тому лист втратить стійкість. При втраті стійкості деформації прогину зосереджуються, як правило, у межах квадратних областей, на які можна розбити пластину (рисунок 9.15).
Крім цих деформацій мають місце кутові деформації від приварки ребер і, пов’язаний з цим, прогин листа між ребрами жорсткості (рисунок 9.16).
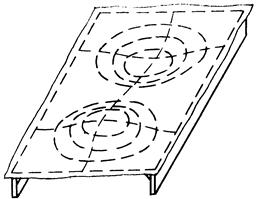
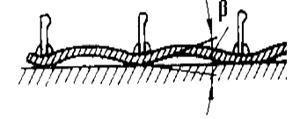
| Рисунок 9.15 – Деформації прогину при втраті стійкості | Рисунок 9.16 – Кутові деформації |
Якщо внутрішні шви виконуються перед зовнішніми, то кути β утворюються тільки за рахунок неповного провару по товщині листа і можуть бути знайдені за графіком 9.1 для відносної величини погонної енергії:
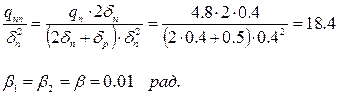
Прогин пластини 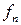 :
:
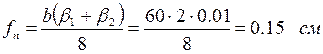
Дата добавления: 2020-03-17; просмотров: 771;











