Напруження і деформації від поздовжніх швів
У попередньому розділі розглядались приклади визначення напружень і деформацій балок при наявності деякого об’єму подовжнього укорочення. Згідно з розділом 3, при виконанні поздовжніх швів об’єм укорочення може бути визначений за формулою (4.18):
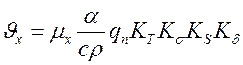 , (5.1)
, (5.1)
де μх = - 0.335;
qп - погонна енергія при наплавленні шва (2.15);
α/сρ - теплофізична характеристика матеріалу;
КТ, Кσ, КS Кδ, - коефіцієнти, що враховують, відповідно, тепловіддачу, наявність напружень у точках, де виконується шов; товщину листа і податливість конструкції.
Таким чином, переміщення від поздовжніх швів у балках можуть бути визначені за формулами попереднього розділу, тобто після введення фіктивних (усадочних) сил за формулою:
Fусі= 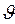 xіЕ, (5.2)
xіЕ, (5.2)
і використання наведених вище залежностей опору матеріалів, або безпосередньо за формулами (4.10), (4.12).
Разом з тим специфіка утворення об’єму подовжнього укорочення при зварюванні потребує деяких уточнень стосовно напружень і положення площі АТ, по якій розподілені залишкові деформації укорочення.
Запишемо відносні деформації у довільній точці перерізу при згинанні балки у двох головних площинах х0у і х0z у вигляді:
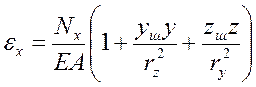 , (5.3)
, (5.3)
де ry , rz - радіуси інерції площі поперечного перерізу відносно головних центральних осей:
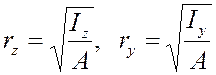 . (5.4)
. (5.4)
Зокрема, деформації по осі шва (у=уш, z=zш):
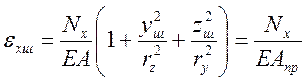 , (5.5)
, (5.5)
де Апр - приведена площа поперечного перерізу:
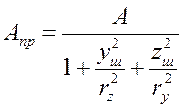 . (5.6)
. (5.6)
Напруження у поперечних перерізах визначаються за формулою:
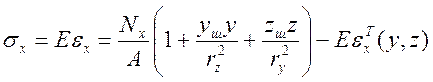 , (5.7)
, (5.7)
де εТx - залишкові пластичні деформації у точках площі.
У розглянутих вище прикладах залишкові напруження вважалися сталими і при згинанні балки відповідно зменшувалися, урівноважуючи напруження, що з'являлись від згинання балки. Специфіка утворення об'єму подовжнього укорочення при зварюванні полягає у тому, що він утворюється одночасно з деформацією балки, і податливість балки впливає на величину напружень. Згідно з прикладом 1.3, при врахуванні податливості закріплення, пряма, визначаюча утворення пружних деформацій стиску, має менший кут нахилу до осі ε, у зв’язку з чим пластичні деформації починаються при більш високій температурі нагріву, тобто ε`S>εS (рисунок 5.1).
Величина пластичних деформацій залежить від податливості конструкції у центрі ваги шва і дорівнює (εш+ε`S). Площа зони пластичних деформацій АS визначається площею криволінійної трапеції abcd (рисунок 5.1) або рівновеликою площею прямокутника a1b1c1d1. Площу АТ можна визначити з умови:
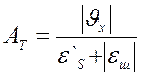 . (5.8)
. (5.8)
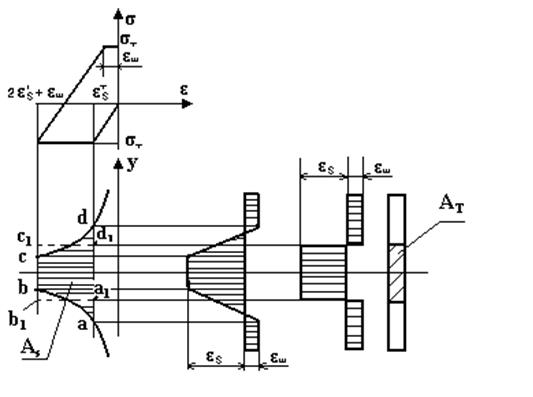
Рисунок 5.1 – Діаграма деформування балки з врахуванням податливості
Після підстановки значень εш (5.5) і 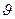 x(5.1),
x(5.1),
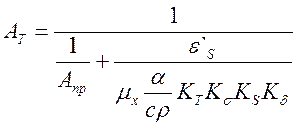 . (5.9)
. (5.9)
Введемо коефіцієнт КΩ=εS/ε`S, який визначає зміну температуру початку пластичних деформацій у районі зварного шва.
Площа АТ, з урахуванням КΩ має вигляд:
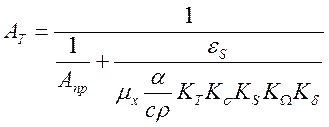 . (5.10)
. (5.10)
Для балок з розвиненою площею поперечного перерізу |εш| << εS, КΩ·КS≈1 і формула для визначення площі АS спрощується,
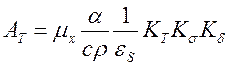 . (5.11)
. (5.11)
Ширина зони пластичних деформацій у перерізі:
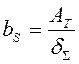 , (5.12)
, (5.12)
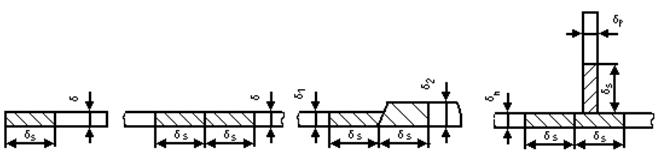
де δΣ - сума товщин елементів, що зварюються (рисунок 5.2).
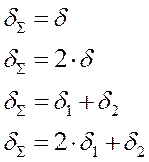
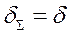
| 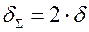
| 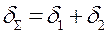
| 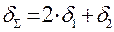
|
Рисунок 5.2 – Ширина пластичних деформацій в залежності від виду зєднання
Маючи значення площі пластичних деформацій АТ, побудову епюри напружень у поперечних перерізах проводять у такій послідовності. Визначають деформацію ε0 у центрі ваги перерізу і εш у центрі ваги шва:
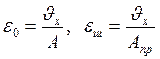 . (5.13)
. (5.13)
Через ці дві точки проводять пряму пружних деформацій від згинання і розтягу балки (пряма ab). Після цього у межах пластичної зони паралельно прямій ab на відстані εS від неї проводять паралельну пряму сd, яка визначає пластичні деформації у зоні АТ. Приклади епюр наведені на рисунку 5.3.
Якщо балка має n–зварних швів і зібрана на прихватках, так що поперечний переріз залишається незмінним при зварюванні, загальні деформації визначаються як сума деформацій від кожного шва окремо:
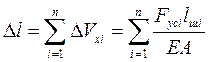 , (5.14)
, (5.14)
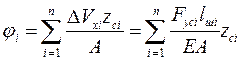 . (5.15)
. (5.15)
Якщо довжина усіх швів lші, співпадає з довжиною балки, можна знайти максимальний прогин
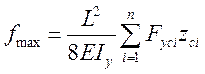 . (5.16)
. (5.16)
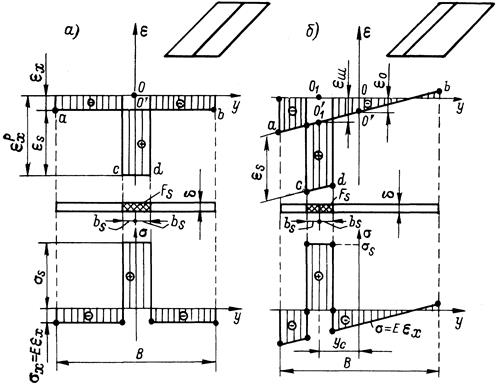
Рисунок 5.3 – Епюри пружніх і пластичних деформацій
У випадку, коли шви різної довжини, доцільно для визначення прогинів скористатись поняттям усадочної сили і, приклавши відповідні сили на кінцях кожного шва, знайти прогин методами опору матеріалів: або методом початкових параметрів, або за допомогою Мора, Кастільяно, Верещагіна і т.п.
Якщо шви виконуються послідовно, для кожного наступного шва необхідно враховувати вплив напружень, які з'явились після виконання попередніх швів. Об'єм подовжнього укорочення наступного шва обчислюється за формулою:
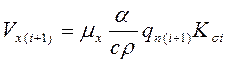 , (5.17)
, (5.17)
де Кσі - коефіцієнт, що враховує вплив попередніх швів на об’єм (і+1)-го шва.
Якщо зони пластичних деформацій АТі частково перекриваються, необхідно враховувати зменшення сумарної площі за допомогою коефіцієнта перекриття швів Кп . Величина коефіцієнта Кп для двох випадків, наведених на рисунку 5.4, визначається за формулами:
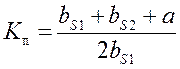 – (Рисунок 5.4 а)
– (Рисунок 5.4 а)
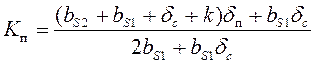 – (Рисунок 5.4 б)
– (Рисунок 5.4 б)
сумарна площа пластичних деформацій визначається за формулою
АТ=АТ1∙kп,
де АТ1 - площа пластичних деформацій від першого шва.
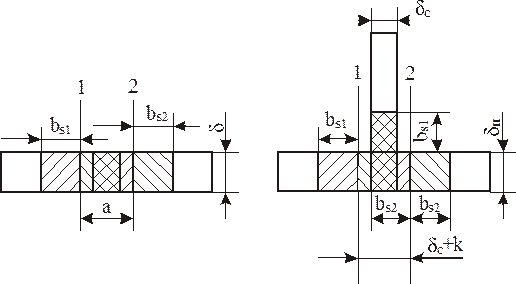
Рисунок 5.4 – Коефіцієнт перекриття швів для стикового та таврового шва
Приклад 5.1. Визначити загальні деформації балки таврового перерізу (рисунок 5.5) від двох кутових неперервних швів, що з’єднують, стінку з полицею. Шви виконуються послідовно погонною енергією qп = 12500 Дж/см. Матеріал балки - маловуглецева сталь, (εS = 0,00125). Довжина балки 10 м.
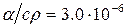
1) Геометричні характеристики площі перерізу:
2)
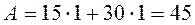 см2,
см2,
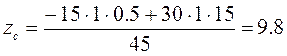 см,
см,
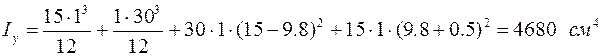
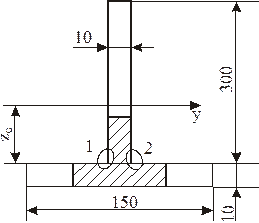
Рисунок 5.5 – Схема балки таврового перерізу
3) Площа і ширина пластичної зони від першого шва
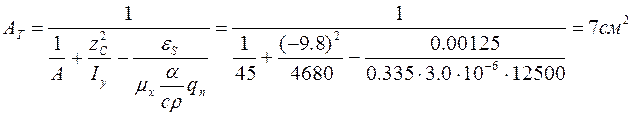
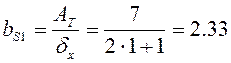 см
см
3) Коефіцієнт, враховуючий перекриття зон швів:
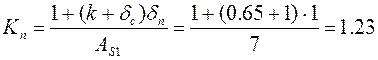
4) Об'єм подовжнього укорочення
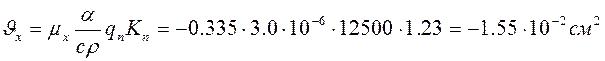
5) Загальні деформації балки:
а) Укорочення центральної осі
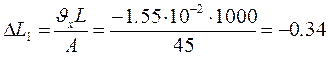 см;
см;
б) взаємний кут повороту крайніх перерізів балки
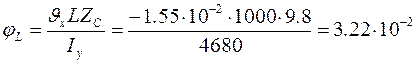 рад;
рад;
в) максимальний прогин
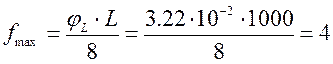 см
см
Приклад 5.2 Визначити загальні деформації балки двотаврового перерізу (рисунок 5.6) від односторонніх швів з погонною енергією qп=10000 Дж/см. Геометричні характеристики площі перерізу А=38 см2, Іу= 6170 см4 . Довжина балки L=10 м. Матеріал - маловуглецева сталь. Двотавр перед зварюванням зібраний на прихватках.
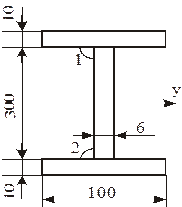
Рисунок 5.6 – Схема балки двотаврового перерізу
Коефіцієнт температуропроводності а =0.1 cм2/c ;
коефіцієнт температуровіддачі b=2*10-3 1/см; α/ср=3,5*10-6 см3/Дж; εS=11,7*10-4.
1) Визначимо коефіцієнт, що враховує вплив тепловіддачі на об’єкт подовжнього укорочення. Параметр π1
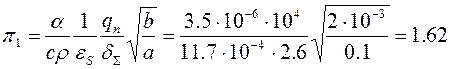 .
.
(Враховано, що δΣ = 1+1+0,6=2,6, рисунок 5.7)
З графіка (3.4) знаходимо КТ=0,85.
Дата добавления: 2020-03-17; просмотров: 807;











