Напруження і деформації, обумовлені об’ємними змінами.

Розглянемо паралелепіпед зі сторонами а, b, l (рисунок 4.1) у системі координат х , у , z . Нехай внаслідок деяких причин (наприклад, нагрівання) довжина сторони l, збільшилась на величину Δl. Назвемо збільшення об’єму паралелепіпеда у напрямку осі х об’ємом подовження, або об’ємом деформації

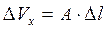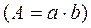, . (4.1)

Об’єм подовження (по­гонний об’єм), що припадає на одиницю довжини,

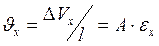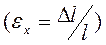, . (4.2)

Якщо погонний об’єм змінюється по довжині l, повний об’єм обчислюється інтегралом:

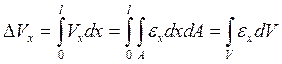. (4.3)

При ε_х=const:

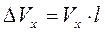. (4.4)

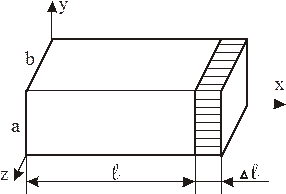
Рисунок 4.1 – Схема паралелепіпеда

Аналогічно можна ввести поняття об’ємів подовження (абo укорочення) у напрямку осей y і z.

Поява об’ємної деформації у вигляді об'ємів подовження (укорочення) призводить до порушення умов рівноваги макрооб’ємів і перерозподілу напружень і деформацій в об’ємі тіла, що, у свою чергу, спричиняє появу переміщень точок об'є­му.

Розглянемо декілька прикладів визначення наслідків по­яви об’ємних змін у конструкціях балок, не акцентуючи увагу на причинах появи цих змін.

Приклад 4.1 Визначити переміщення і напруження у стержні прямокутного перерізу при наявності об’єму подовжнього укоро­чення V_x=ε^ТА_Т, (А_Т=Вּh), рівномірно розподіле­ного по довжині стержня L (рисунок 4.2).

Наявність об’єму подовжнього укорочення V_x призводить до появи у перерізах стержня врівноваженої системи напружень і деформування стержня у цілому.

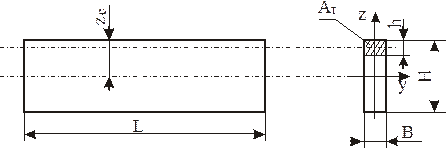
Рисунок 4.2 – Схема стержня прямокутного перерізу

Вважаючи, що поперечні перерізи стержня залишаються плоскими і перпендикулярними осі стержня, деформацію на рівні z запишемо у вигляді:

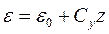, (4.5)

де ε₀ - деформація у точках на осі стержня, C_y - кри­визна стержня у площині z0x.

Напруження, згідно з законом Гука[3]:

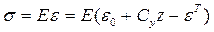. (4.6)

Умови рівноваги для системи напружень у перерізі:

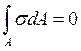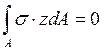, , (А=ВּН), (4.7)

або після підстановки напружень (4.6)

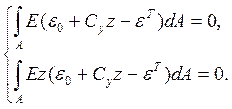(4.8)

Розв'язуючи цю систему рівнянь відносно ε₀ і С_у, одержимо:

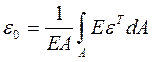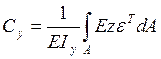, , (4.9)

де A - площа поперечного перерізу,

І_у, - осьовий момент інерції площі А відносно осі у.

Враховуючи вираз для об’єму подовжнього укорочення V_x=A_Tּε^Т формули для деформації ε₀ і кривизни С_у можна переписати у вигляді:

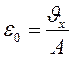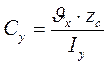, . (4.10)

Укорочення і прогин балки визначаються за формулами:

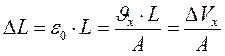, (4.11)

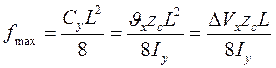, (4.12)

де ΔV_х= 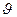_хl_ш - повний об’єм подовжнього укорочення (l_ш=L).

У випадку, коли довжина шва менше довжини балки, залеж­ність для укорочення ΔL має такий же вигляд (4.11), а для визначення максимального прогину необхідно врахувати, що кривизна зосереджується на довжині l_ш, а інші ділянки балки будуть залишатися прямолінійними (рисунок 4.3).

Прогин балки не важко визначити, маючи значення взаєм­ного кута повороту крайніх перерізів ділянки l_ш :

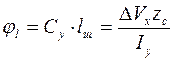. (4.12а)

Звернемо увагу на те, що взаємний кут повороту крайніх перерізів ділянки l_ш, співпадає з кутом повороту крайніх перерізів балки. Таким чином, кути повороту крайніх перерізів балки обчислюються за формулою (4.12а) незалежно від довжини шва і розміщення його по довжині балки. Цей факт використо­вують при визначенні прогинів від поперечних швів, регуляр­но розміщених по довжині балки (див. розділ 6).

При визначенні прогинів і переміщень перерізів балки ви­користовується методика, що базується на понятті фіктивної або усадочної сили. Повернемось для пояснення цього прийому до формул (4.8). Інтеграли у цих формулах мають розмір­ність, відповідно, сили і моменту.

Позначаючи:

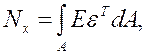
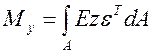, (4.13)

формули для деформації ε₀ і кривизни С_у запишемо у вигляді:

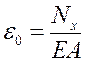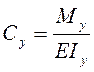, , (4.14)

де N_х і M_y - рівнодіючі внутрішніх сил у перерізах стержня[4]:

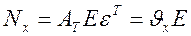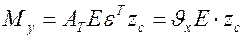, . (4.15)

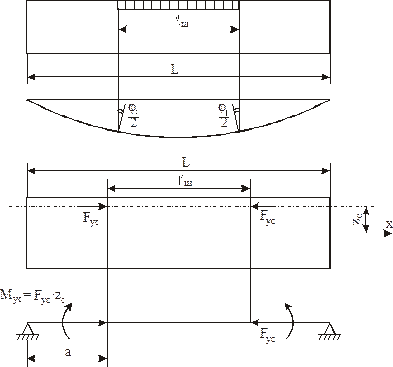
Рисунок 4.3 – Розрахункова схема балки

Будемо розглядати деформації (4.14) як результат дії деякої позацентрової прикладеної сили F_у з координатою z_c (рисунок 4.4). Знак сили співпадатиме зі знаком деформацій об’єму укорочення, тобто сила буде стискаючою,

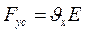. (4.16)

Відповідна розрахункова схема зображена на рисунку 4.3в. Запишемо диференціальні рівняння розтягу-стиску і згину:

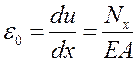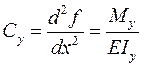, . (4.17)

Інтеграли рівнянь (4.17) мають вигляд:

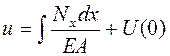, (4.18)

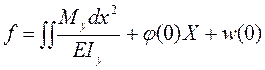, (4.19)

де u(0), φ(0) - переміщення і кут повороту перерізу X=0.

При наявності однієї пари сил F_yс (рисунок 4.3), внут­рішні сили N_х і М_y мають вигляд:

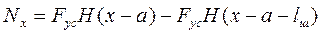, (4.20)

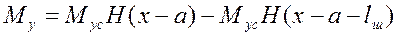, (4.21)

де Н(х-а) - функція Хевісайда:

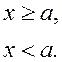
Після підстановки (4.20) і (4,21) у (4.18) і (4.19) і інтегрування, одержимо формули для обчислення поздовжніх переміщень перерізів і прогинів балки:

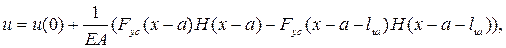(4.22)

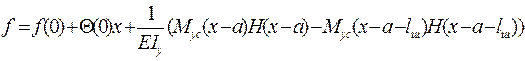, (4.23)

Якщо швів декілька і довжина їх різна, формули (4.22), (4.23) приймуть вигляд:

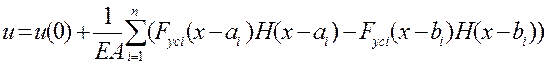, (4.24)

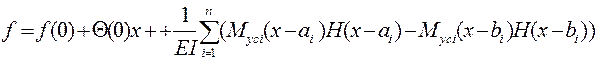,(4.25)

де а_і , в_i - координати початку і кінця і-го шва;

N_ci, М_сі - умовні сили, діючі у перерізах х= а_і і х=в_і.

Формули (4.24) (4.25) дозволяють побудувати точні функ­ції переміщень u і f не вдаючись до геометричних побудов.

Необхідно зазначити, що введення поняття умовних сил є корисним для аналізу напружень у складних стержневих кон­струкціях, зокрема у ступінчастих балках, рамах і т.п.. Однак для цих випадків замість формул методу початкових параметрів (4.24), (4.25) доцільно скористатись енергетичними методами.

Розглянемо докладніше питання про напруження. У кожній точці перерізу напруження складається з трьох доданків: від стиску, згинання і напружень, пов'язаних з деформаціями подовжнього укорочення (рисунок 4.4)

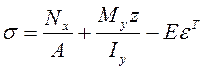. (4.26)

Сумарна епюра напружень побудована на рисунку 4.4г, Таким чином, для визначення переміщень і напружень, обумовлених появою об’ємів подовжнього укорочення, необхід­но визначити усадочні сили, пов’язані з кожним швом, за формулою (4.15) і використати відповідні формули опору мате­ріалів для балок, навантажених цими силами.

Нагадаємо, що переміщення можна також визначити, не вводячи поняття усадочної сиди (формули (4.10), (4.12)) і у більшості випадків це виявляється навіть зручнішим, зважаю­чи на неоднозначність поняття "усадочна" сила (див. розділ 5).

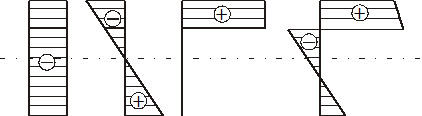
а) б) в) г)

а)–Епюра напруження від стиску;

б)– Епюра напруження від згину;

в)– Епюра напружень пов'язаних з деформаціями подовжнього укорочення;

г)–сумарна епюра.

Рисунок 4.4 – Епюра напружень

Приклад 4.2 Визначити напруження у поперечник перерізах стержня кутового профілю від об’єму подовжнього укорочення ΔV_х =А_Тε^ТL (рисунок 4.5)

Рисунок 4.5 – Схема стержня кутового профілю

Згідно з припущенням про справедливість гіпотези плос­ких перерізів, деформації у перерізі визначаються за формулою:

ε=ε₀+C_yz+C_zy, (4.27)

де Су , Сz - кривизни у площинах x0z, z0у відповідно.

Напруження з урахуванням об’єму укорочення:

σ=Е(ε₀+ C_yz+C_zy)-Еε^Т. (4.28)

Умова рівноваги напружень у перерізах:

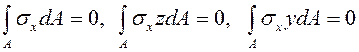. (4.29)

Після підстановки (4.28) у (4.29) матимемо систему рів­нянь для визначення ε₀, Су і Сz , з якої по аналогії з по­переднім прикладом одержимо:

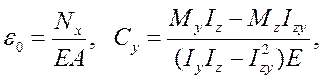
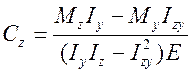, (4.30)

де І_z, І_у, І_zу - моменти інерції площі поперечного перерізу відносно осей z і у,

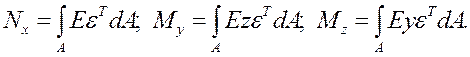(4.31)

З урахуванням значення об'єму укорочення:

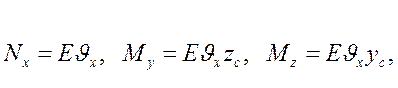(4.32)

де .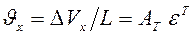

Зусилля N_x, М_y, М_z можна вважати результатом дії фіктивної (усадочної) сили F_yc= E 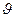_х у кінцевих перерізах балки у точках з координатами z_с і у_с.

Напруження у перерізах балки, згідно з (4.28):

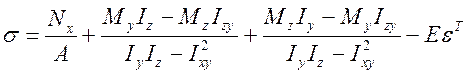, (4.33)

Для побудови епюри напружень необхідно визначити геометричні характеристики площі перерізу в осях у, z, сили N_х, М_у і М_z, врахувавши, що при від’ємних ε^Т ці сили бу­дуть від’ємними.

Кожна з чотирьох складових напружень (4.33) побудована на рисунку 4.6 (а - г ).

Залежність (4.33) можна спростити, якщо провести усі розрахунки у головних осях площі перерізу балки.

При цьому відцентровий момент дорівнюватиме нулю, і фор­мула для напружень прийме вигляд:

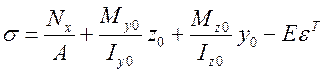. (4.35)

а) б) в) г)

а)–Епюра напруження від стиску;

б)– Епюра напруження від згину;

в)– Епюра напружень пов'язаних з деформаціями подовжнього укорочення;

г)–сумарна епюра.

Рисунок 4.6 – Епюри напружень

У (4.34) моменти І_у0 і І_z0 – є головними центральними мо­ментами, а z₀ і у₀ - координати точки перерізу у головних центральних осях (рисунок 4.7).

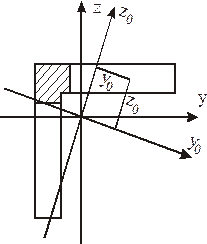
Рисунок 4.7 – Переріз балки відносно головних осей

Зазначимо, що моменти М_у0 і М_z0 визначаються також у головних осях.

Таким чином, у загальному випадку розміщення об’єму укорочення можна скористатись поняттям усадочної сили, виз­начаючи її за формулою (4.25) і прикладаючи у центрі ваги площі А_Т , Після визначення головних осей і моментів інер­ції, а також координат центра ваги площі А_Т у цих осях, напруження знаходиться за формулою (4.34).