Вплив поздовжніх деформацій
Якщо врахувати, що одночасно з поперечними розвиваються поздовжні деформації, повні поперечні деформації на етапі нагрівання будуть складатися з трьох доданків:
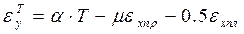 , (3.23а)
, (3.23а)
де εхпр, εхпл – відповідно, пружна і пластична деформація у напрямку осі х;
μ і 0.5 - коефіцієнти Пуассона.
Укорочення смуги у відповідності до (3.21):
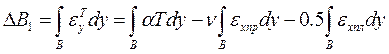 . (3.24)
. (3.24)
Перший інтеграл обчислений вище – (3.20); другий дорівнює нулю, оскільки пружні деформації урівноважені у перерізі; третій (сума пластичних деформацій у напрямку осі Х) може бути наближено прийнятим 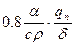 [2]. Таким чином:
[2]. Таким чином:
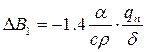 . (3.25)
. (3.25)
Нагадаємо, що ΔВ1 – це деформації, які реалізувались у вигляді пластичних деформацій у напрямку осі шва (розмір при цьому не змінюється). (Порівняйте з прикладами першого розділу).
При охолодженні у зв’язку з тим, що на сторонах 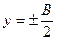 пластини не закріплені, розміри В починають зменшуватись. Якщо не враховувати поздовжніх пластичних деформацій, це зменшення дорівнюватиме ΔВ1. Поздовжні пластичні деформації після охолодження εхпл є стискаючими і визначаються об’ємом подовжнього укорочення
пластини не закріплені, розміри В починають зменшуватись. Якщо не враховувати поздовжніх пластичних деформацій, це зменшення дорівнюватиме ΔВ1. Поздовжні пластичні деформації після охолодження εхпл є стискаючими і визначаються об’ємом подовжнього укорочення 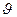 х. З урахуванням ефекту Пуассона вони зменшують величину ΔВ1, на ΔВ'1
х. З урахуванням ефекту Пуассона вони зменшують величину ΔВ1, на ΔВ'1
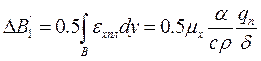 .
.
Таким чином величина укорочення смужки dx становить:
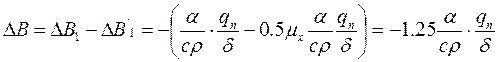 . (3.26)
. (3.26)
Погонний об’єм поперечного укорочення:
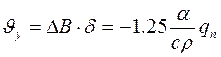 . (3.27)
. (3.27)
Як видно з (3.27), об’єм поперечного укорочення відрізняється від об'єму подовжнього укорочення величиною коефіцієнта (μх=-0,335, μу=-1,25). Одержане значення μy є наближеним, оскільки при його обчисленні не враховувались зміни форми температурних кривих у перерізі при нагріванні-охолодженні. Більш коректно коефіцієнт μу можна визначити, скориставшись графіком на рисунку 3.13 [2], за формулою μу=1+кμ
Укорочення ΔВ можна записати так:
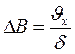 . (3.28)
. (3.28)
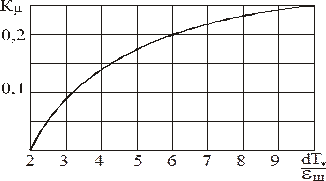
Рисунок 3.13 – Залежність коефіцієнта К  від параметру
від параметру 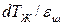
Дата добавления: 2020-03-17; просмотров: 820;











