Алгоритмы трассировки печатного монтажа

Алгоритмические методы трассировки печатного монтажа существенно зависят от конструкции коммутационного поля и могут быть разделены на два больших класса [8,9].

К первому классу относятся так называемые графотеоретические методы трассировки. Эти методы используются для топологического проектирования конструкций электронных устройств, для которых задачи размещения и трассировки решаются совместно (односторонние и двухсторонние печатные платы с микросхемами и навесными радиоэлементами, гибридные микросхемы и т.д.). Так как совместное решение задач размещения и трассировки на практике затруднено из-за больших затрат машинного времени, то алгоритмы этого класса используются для разработки устройств, выпускаемых большой серией.

Ко второму классу относятся последовательные методы трассировки, в которых предпочтение отдается метрическому аспекту задачи, предполагающему учет конструктивных размеров элементов, соединений и коммутационного поля. К этому классу относятся волновой алгоритм Ли и его модификации, алгоритмы трассировки по магистралям и каналам, ряд комбинированных алгоритмов, а также большая группа эвристических алгоритмов. Большое распространение алгоритмов, основанных на идеях Ли, определяется прежде всего возможностью их адаптации к различным конструктивно-технологическим особенностям печатных соединений. Основным недостатком волновых алгоритмов являются значительные затраты времени и памяти ЭВМ.

Отметим, что с помощью программ трассировки удается развести до 95…99 % всех соединений. Оставшиеся неразведенные соединения конструктор должен развести вручную.

При решении задачи трассировки обычно используют следующие критерии качества: минимум суммарной длины соединений; минимум пересечений проводников; минимум числа переходов между слоями; минимум углов в соединении; степень "прижатия" к ранее проведенным соединениям. Следует отметить, что ни один из указанных критериев не является определяющим для получения качественной трассировки.

Для решения задач трассировки обычно используется модель МКП в виде ДРП (МКП1) либо дискретно-графовые модели МКП3 и МКП4. Модель устройства обычно использует тип МУ4.

Сформулируем задачу трассировки печатных соединений. На коммутационном поле задано своими координатами (x_i, y_i) множество конструктивных модулей E={e₁, …, e_n}. Выводы этих компонентов образуют множество C из связанных подмножеств: C={C₁, …, C_m}, причем каждое i-е подмножество C_i соединяет ½C_i½=n_i выводов модулей, соединенных одной цепью u_i. Кроме того, заданы расположения контактных групп разъема, а также требования к топологии печатной платы. Требуется с учетом заданных конструктивно-технологических ограничений соединить контакты модулей внутри каждого подмножества C_iÌC так, чтобы соединения отвечали критерию минимума суммарной длины соединений.

Трассировка печатных соединений выполняется в несколько этапов: построение деревьев печатных соединений по слоям печати, определение порядка трассировки проводников в слое и собственно трассировка. Рассмотрим эти этапы подробнее.

При проектировании печатных соединений применяются связывающие деревья в основном двух видов: кратчайшие связывающие сети либо деревья специального вида, называемые деревьями Штейнера. Кратчайшие связывающие сети могут строиться с помощью алгоритма Прима по кратчайшим расстояниям, как для проводного монтажа, либо в ортогональной метрике, обычно используемой в печатных платах.

В отличие от кратчайших связывающих сетей дерево Штейнера может содержать добавочные вершины, позволяющие уменьшить длину соединений и упростить их форму. Поскольку при машинной трассировке печатных соединений используется в основном ортогональная метрика, остановимся на задаче построения дерева Штейнера в такой метрике. Известно, что в ортогональной метрике при отыскании местоположения дополнительных вершин можно ограничиться узлами ортогональной сетки, построенной на n_i=½C_i½ основных вершинах, а степень вершин такого дерева ограничивается соотношением 3£g£4.

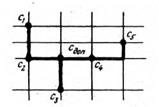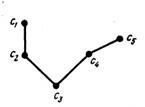
Для примера на рис. 7.4 показан вариант дерева печатного соединения в виде кратчайшей связывающей сети, а на рис. 4.4, б – вариант дерева Шнейдера, дополнительные вершины которого построены в узлах ортогональной сетки, проходящей через основные вершины.

а) б)

в) г)

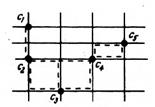
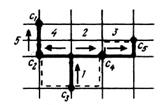
Рис. 7.4. Трассировка печатного монтажа: а – кратчайшая связывающая сеть, б – дерево Шнейдера в ортогональной метрике, в, г – построение дерева Шнейдера с помощью алгоритма Прима

При небольшом числе n_i для отыскания дополнительных вершин c_q в принципе можно воспользоваться методом сокращенного перебора. При большом числе вершин дерева метод перебора требует больших затрат машинного времени, поэтому используют эвристические алгоритмы, позволяющие получить близкое к оптимальному решение.

Суть одного из таких алгоритмов заключается в построении на ортогональной сетке с помощью алгоритма Прима кратчайшего связывающего дерева с дублированием ветвей, имеющих минимальную длину. На втором этапе построения дерева выбираются по очереди все соединенные вершины, анализируются ветви, инцидентные данным вершинам, и из них оставляются только те, которые имеют наибольшие общие участки, остальные отбрасываются. Последовательность построения дерева Штейнера для примера 7.4, а показана на рис. 7.4, в, г.

Если алгоритм трассировки предусматривает последовательную реализацию соединений, то для построения дерева Штейнера может использоваться модификация волнового алгоритма Ли.

Расслоение печатного монтажа до трассировки основано на анализе схемы соединений для выделения той группы соединений, которые не могут быть расположены на одной плоскости из-за неизбежных пересечений. Один из способов проведения такого анализа состоит в разбиении графа, моделирующего устройство, на минимальное число планарных подграфов (планарным называется граф, если для него существует плоский чертеж без пересечения ветвей), которые могут быть трассированы в слое без пересечений. Основная сложность в этом случае заключается в построении графовой модели устройства, учитывающей метрические параметры МКП.

Чаще при трассировке задача расслоения решается при заданной геометрии деревьев отдельных соединений. В этом случае для расслоения обычно строится граф пересечений G_П(S_П, V_П), вершины которого S_П соответствуют отдельным проводникам деревьев печатных соединений, а ветви V_П – их пересечениям. На рис. 7.5, а представлена система проводников, образующих деревья соединений, а на рис. 7.5, б – соответствующий ей граф пересечений. Считая, что раскраска вершин графа пересечений G_П приводит к расположению проводника в соответствующем слое, задачу расслоения можно решить , раскрасив граф пересечений G_П в минимальное число цветов так, чтобы смежные вершины были окрашены в разные цвета (минимальное число цветов, которым необходимо пометить вершины графа, чтобы смежные вершины были окрашены в разные цвета, называют хроматическим числом графа b). Число слоев печати для трассировки пересечений будет равно b–1. Для большого числа слоев печати применять такую методику затруднительно, так как в настоящее время отсутствуют общие критерии для определения хроматического числа графа, а эвристические алгоритмы часто дают завышенное значение b. Поэтому в настоящее время часто производят двухцветную или многоцветную окраску графа G_П, такую, чтобы суммарное число ветвей, соединяющих одноцветные вершины, было минимально, т.е. было минимальным количество неустранимых пересечений при трассировке.

При ортогональной трассировке возможно тривиальное расслоение печатного монтажа без пересечения проводников, когда все горизонтальные отрезки соединений помещаются в одном поле, а вертикальные – в другом. В точках изгиба соединений размещаются контактные переходы из слоя в слой (рис. 7.6). Однако в этом случае возникает избыточное число переходов между слоями, что снижает надежность и удорожает печатную плату.

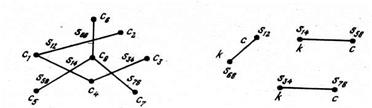а) б)

Рис. 7.5. Расслоение печатного монтажа с помощью графа пересечений: а – деревья соединений, б – граф пересечений и его раскраска

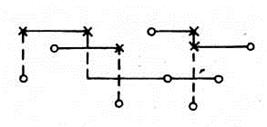Рис. 7.6. Ортогональное расслоение печатного монтажа: – 1-й слой, --- 2-й слой, Х – переход, О – контакт

В ряде работ [2,9] рассматриваются более общие случаи задачи расслоения, включающие минимизацию числа переходов между слоями и пересечений проводников в слое.

Подавляющее большинство алгоритмов трассировки выполняет задачу построения проводников лишь для элементарных соединений, т.е. соединений между эквипотенциальными контактами, поэтому для реализации автоматической трассировки проводников необходимо определить очередность их трассировки. Наиболее распространено упорядочение соединений, основанное на их длине: вначале трассируются соединения, имеющие наибольшую длину, затем короткие, либо наоборот. Статистика показывает, что любая из тактик упорядочивания по длине приводит примерно к одинаковым результатам трассировки с точки зрения числа пересечений проводников.

Более тонкие методы упорядочения трассировки связаны с учетом взаимного влияния соединений, когда наряду с метрическими характеристиками используются и топологические характеристики взаимного расположения соединений в МКП.

Перейдем теперь к рассмотрению волнового алгоритма трассировки Ли. Этот алгоритм использует дискретные модели МКП по типу МКП1 и графовые модели устройства вида МУ4.

Рассмотрим топографическую модификацию волнового алгоритма трассировки. При трассировке печатных проводников этой модификацией волнового алгоритма все ДРП подразделяются на занятые, ДРП с поднятым рельефом и свободные. Занятыми считаются ДРП, в которых расположены уже трассированные проводники, и ДРП, запрещенные по тем или иным соображениям для прокладки печатных проводников. Занятым ДРП заранее присваивается большой вес, который не может быть достигнут при распространении волнового фронта. ДРП с поднятым рельефом – это ячейки МКП, расположенные рядом с занятыми и соприкасающиеся с ними хотя бы одной стороной. ДРП, расположенным рядом с занятыми, присваивается вес 2, а соседним с ними – вес 1, если они не имеют более высокого рельефа.

На первом этапе работы волнового алгоритма на множестве свободных ячеек от первого контакта трассируемой цепи – источника – ко второму контакту – приемнику – распространяется числовая волна. При этом последовательно шаг за шагом строится очередной фронт волны, в котором каждому ДРП присваивается вес по формуле p_t=p_t-1+e+r, где p_t и p_t-1 – веса ДРП в t-м и (t-1)-м фронтах, e – некоторая функция, в простейшем случае равная +1, r – вес, заранее присвоенный ДРП при формировании рельефа, t – фронт волны, распространяющейся из ДРП, принадлежащих (t–1)-му фронту, только на соседние ячейки, имеющие с ячейками предыдущего фронта общую сторону.

Чтобы исключить неопределенности в выборе веса ДРП, которые могут возникнуть при распространении числовой волны и при проведении трассы, вводят путевые координаты, задающие предпочтительное направление движения трассы, например вверх, направо, вниз, влево.

Процесс построения волны продолжается до тех пор, пока ее расширяющийся фронт не достигнет второго контакта – приемника – или на каком-то шаге не найдется ни одной свободной ячейки, которая могла бы быть включена в очередной фронт, что соответствует невозможности проведения трассы при заданных ограничениях.

Если в результате распространения волны по свободным ДРП коммутационного пространства числовая волна достигнет второго контакта трассируемой цепи – приемника, то процесс распространения волны прекращается и начинается второй этап трассировки – проведение пути. Для этого необходимо, начиная от ДРП, в котором располагается второй контакт – приемник трассируемой цепи, двигаться в направлении, противоположном направлению распространения волны, последовательно переходя от ДРП с большим весом p_t к соседнему ДРП с меньшим весом p_t-1, следя за тем, чтобы значения веса монотонно убывали. Ячейки ДРП, выделенные в ходе указанного процесса, и определяют искомое оптимальное соединение.

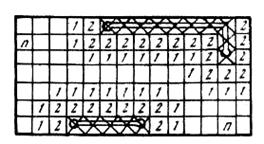
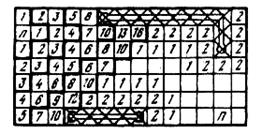
На рис. 7.7, а показана плата с ДРП и рельефом, на рис. 7.7, б – процесс распространения числовой волны по ДРП платы, на рис. 7.7, в – процесс проведения пути.

а)

б)

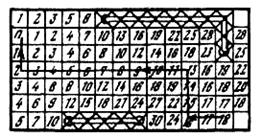в)

Рис. 7.7. Трассировка печатных соединений волновым алгоритмом: а – рельеф платы, б – распространение фронтов числовой волны, в – проведение трассы

Трассировка цепей, содержащих более двух контактов, проводится в несколько этапов. На каждом этапе к цепи присоединяется один контакт, и источником волны для следующего этапа становятся все заранее проведенные проводники, что позволяет получить близкую к минимально возможной суммарную длину всех проводников, т.е. сформировать проводники в виде дерева Штейнера.

В реальных программах волновой алгоритм обычно разделяют на три подалгоритма: корректировки рельефа, распространения волны и проведения трассы. Назначение подалгоритма корректировки рельефа состоит в том, чтобы создать начальный рельеф вокруг контактов, нанесенных на ДРП, и на последующих этапах трассировки создать рельеф около вновь проведенных соединений.

Подалгоритм распространения волны последовательно шаг за шагом строит фронты числовой волны в свободных ДРП и ДРП с поднятым рельефом до достижения ими контакта-приемника.

Подалгоритм проведения трассы осуществляет соединение найденного контакта цепи с основной цепью или исходным контактом. Его работа во многом подобна работе подалгоритма распространения волны.

Алгоритм 7.9. Построение числовой волны по свободным ДРП

Шаг 1. Определяется ДРП – источник волны, соответствующий одному из контактов трассируемого соединения, и ДРП – приемник волны. ДРП – источник волны – полагается нулевым фронтом числовой волны.

Шаг 2. Последовательно в порядке заданных путевых координат просматриваются ячейки, соседние с ячейками предыдущего фронта числовой волны. Если ячейка свободна либо с поднятым рельефом, то ее вес увеличивается на единицу. Если свободные ДРП перед фронтом волны отсутствуют, то переход к шагу 4.

Шаг 3. Проверяется, достигнут ли ДРП – приемник волны, соответствующий второму контакту трассируемого соединения в очередном фронте числовой волны. Если нет, то переход к шагу 2.

Шаг 4. Подготовка информации для алгоритма проведения трассы.

Приведем теперь пошаговое описание работы подалгоритма построения трассы проводника.

Алгоритм 7.10.Построение трассы проводника

Шаг 1. ДРП, соответствующий ячейке-приемнику волны, помечается как абсолютно занятый. ДРП заносится в список ячеек, по которым пройдет трасса проводника.

Шаг 2. Просматриваются ДРП, соединение с последним включенным в список трассы ДРП.

Шаг 3. Если вес ДРП меньше веса последнего ДРП, включенного в трассу, на единицу, то ДРП помечают как абсолютно занятый и заносят в список дискретов, по которым пройдет трасса.

Шаг 4. Проверяется, не достигнут ли ДРП – источник числовой волны с нулевым весом, если условие не выполнено, то переход к шагу 2.

Шаг 5. По дискретам, занесенным в список для проведения трассы проводника, проводят трассу и поднимают рельеф ДРП вокруг них для проведения следующих трасс.

Структура волнового алгоритма позволяет оптимизировать соединения по различным критериям: количеству пересечений, поворотов проводника, степени приближения проводника к уже проведенным соединениям, минимизации длины соединений за счет модификации распространения числовой волны и построения трассы соединения. Описание этих модификации алгоритма можно найти в [9, 10].